时序分析学习笔记(二)

前言
在上一篇文章[时序分析学习笔记(一)]中,笔者整理了时序分析这门课前两周的课程内容笔记,由于博客目录存在容量上限,之后的内容目录会无法显示,因此为了美观起见,在此重开一篇文章,作为该系列的第二部分
当然,目前课程还未结束,本文会随着课程进度,同步更新。
于2022年5月3日完结
蒙特卡洛模拟(Monte Carlo Simulation)
这个概念本质上就是:已知一个概率分布时,使用计算机模拟一系列的“实际值”来使用。
这部分内容应用详情参见[时间序列案例分析(一)——Lac Leman Festival De La Musique]中的五、六两题。
指数平滑法(Exponential Smoothing Method)
大部分时序数据可以被分为两类:信号(Signal)、噪音(Noise)。它们时常是交织在一起的。
平滑(Smoothing)是一种尽量分离信号和噪音的方法,主要方式是将当前数据与过去关联。
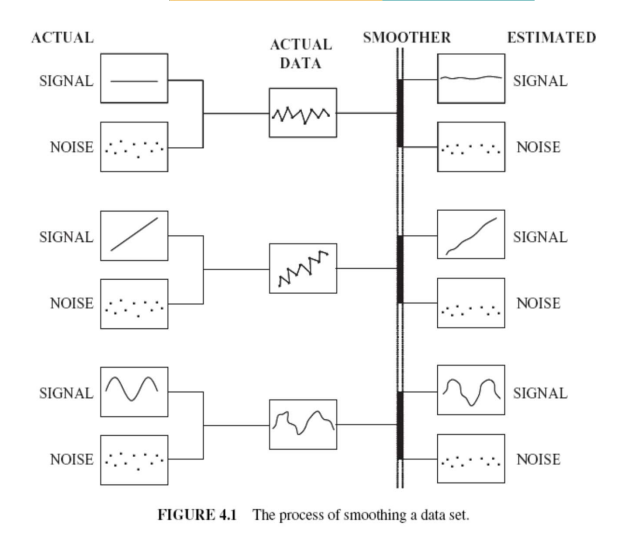
简单指数平滑(Simple Smoothing Method)
简单指数平滑,也可叫一次指数平滑,将历史每一期的数据分别赋予权重,来预测当期数据。其中越近的数据权重越大:
其中通过简单的数学运算,可以知道各项权重的总和为1:
$\alpha +\alpha (1-\alpha)+\alpha (1-\alpha)^2+\alpha (1-\alpha)^3+…+\alpha (1-\alpha)^t+…$
$=\alpha (1+(1-\alpha)+(1-\alpha)^2+1-(\alpha)^3+…$
$=\frac{\alpha}{1-(1-\alpha)}$
$=1$
| Forecast equation | $\hat{y}{T+1 \mid T}=l{T}$ |
|---|---|
| Smoothing equation | $l_{T}= \alpha y_{T}+(1-\alpha)(l_{T-1})$ |
其中,$l_{T}$是在时间$T$时的平滑值。
通过将上述形式迭代,我们可以把它化为加权平均形式:
$$\hat{y}{T+1 \mid T}=\sum{j=0}^{T-1} \alpha (1-\alpha)^{j}y_{T-j}+(1-\alpha)^{T}l_{0}$$
当然,为啥权重要这么设计,本人的数学知识就并不足以解释了,无论如何,这个模型就是这么建的,本学渣就不刨根问底了。可以看出,随着$\alpha$的值变大,我们赋予近期的数据更大的权重,而随着$\alpha$的值变小,我们赋予过去的数据更大权重。
一般而言,当时间数列无明显的趋势变化时,使用这一方法。
我们将这里的$\alpha$称为平滑系数(Smoothing Parameter),它其实就是机器学习中的超参;$l_{0}$则是设定的初始值。
调参的指标我们可以使用SSE:
$$SSE=\sum_{t=0}^{T} (y_{t}-\hat{y}_{t \mid t-1})^2$$
纯数学的东西,没啥大的意义,反正公式都是今天看明天忘,但无论如何,记录在这里表示自己在某一时点学过……
具体使用:
1 | library(fpp2) |
二次指数平滑(Double Exponential Smoothing Method)
对于许多有趋势性的时序数据,简单平滑法并不能很好地进行预测,如:
1 | fc <- ses(elecsales) |
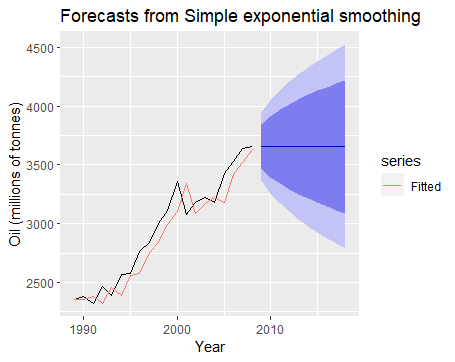
在上图的例子中,我们不难发现,源数据集有着向上的运动趋势,然而通过简单平滑出的预测数据则失去了趋势特征,为了解决这个问题,我们引入了趋势特征,发展出了二次平滑法。同时,二次平滑也有不同的方式。
霍尔特法(Holt Linear Method)
霍尔特二次指数平滑法的形式如下:
| Forecast | $\hat{y}{T+h \mid T}=l{t}+hb_{t}$ |
|---|---|
| Level | $l_{T}= \alpha y_{T}+(1-\alpha)(l_{T-1}+b_{T-1})$ |
| Tred | $b_{T}=\beta (l_{T}-l{T-1})+(1- \beta)b_{T-1}$ |
纯数学的东西,没啥大的意义,反正公式都是今天看明天忘,但无论如何,记录在这里表示自己在某一时点学过……
使用方法:
1 | air <- window(ausair, start=1990) |
也可以用pipeline实现:
1 | window(ausair, start=1990) %>% |
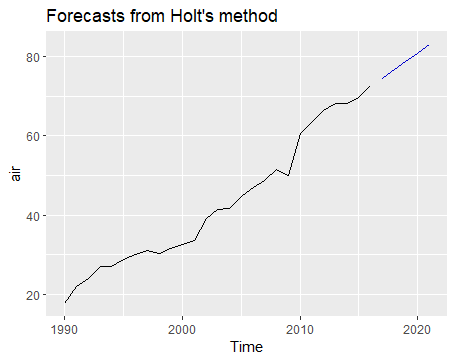
可以看出,此模型将趋势纳入了拟合曲线中。
阻尼法(Damped Trend Method)
当数据的趋势并非保持线性,而是逐步减少时,我们可以在霍尔特法的基础上引入一个阻尼系数来拟合。
| Forecast | $\hat{y}{T+h \mid T}=l{T}+(\phi +\phi^2 +…+\phi^{h})b_{T}$ |
|---|---|
| Level | $l_{T}= \alpha y_{T}+(1-\alpha)(l_{T-1}+\phi b_{T-1})$ |
| Tred | $b_{T}=\beta (l_{T}-l{T-1})+(1- \beta)\phi b_{T-1}$ |
其中,$0 < \phi < 1$
当 $ \phi =1$ 时,便成为了上述的霍尔特模型。
$ \phi $越小,趋势收敛的就越快。
对于短期数据,拟合曲线显示出趋势性,对于长期数据,预测则近似常数。
纯数学的东西,没啥大的意义,反正公式都是今天看明天忘,但无论如何,记录在这里表示自己在某一时点学过……
使用方法:
1 | window(ausair, start=1990) %>% |
对比图:
1 | fc <- holt(air, h=100) |
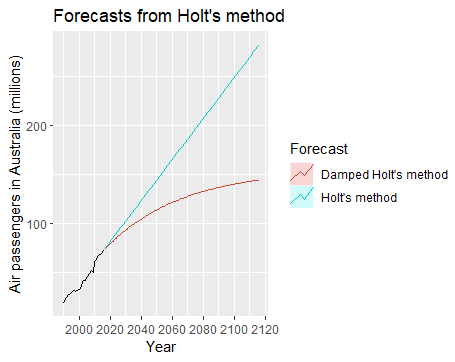
可以直观看出两种二次平滑的不同。
三次指数平滑(Triple Exponential Smoothing Method)
在上述的二次平滑中,我们可以相对有效的拟合出数据的趋势,然而面对季节性数据,则难以有效处理。于是在这种需求下便有了加入了季节考量的三次指数平滑法。
霍尔特-温特斯累加法(Holt-Winters’ Additive Method)
首先不得不吐槽这个翻译,这个温特斯中的“斯”竟然也要翻译出来,实在太丑陋了…
累加法的方程形式如下:
| Forecast | $\hat{y}{T+h \mid T}=l{T}+hb_{T}+s_{T+h-m(k+1)}$ |
|---|---|
| Level | $l_{T}= \alpha (y_{T}-s_{T-m})+(1-\alpha)(l_{T-1}+b_{T-1})$ |
| Tred | $b_{T}=\beta (l_{T}-l{T-1})+(1- \beta)b_{T-1}$ |
| Seasonal | $s_{T}=\gamma (y_{T}-l_{T-1}-b_{T-1})+(1-\gamma)s_{T-m}$ |
其中,m为季节周期,比如4表示一年4季度。
纯数学的东西,没啥大的意义,反正公式都是今天看明天忘,但无论如何,记录在这里表示自己在某一时点学过……
霍尔特-温特斯累乘法(Holt-Winters’ Additive Method)
累乘法的方程形式如下:
| Forecast | $\hat{y}{T+h \mid T}=(l{T}+hb_{T})s_{T+h-m(k+1)}$ |
|---|---|
| Level | $l_{T}= \alpha \frac{y_{T}}{s_{T-m}}+(1-\alpha)(l_{T-1}+b_{T-1})$ |
| Tred | $b_{T}=\beta (l_{T}-l{T-1})+(1- \beta)b_{T-1}$ |
| Seasonal | $s_{T}=\gamma \frac{y_{T}}{(l_{T-1}-b_{T-1})}+(1-\gamma)s_{T-m}$ |
纯数学的东西,没啥大的意义,反正公式都是今天看明天忘,但无论如何,记录在这里表示自己在某一时点学过……
使用方法以及与累加法的区别:
1 | aust <- window(austourists,start=2005) |
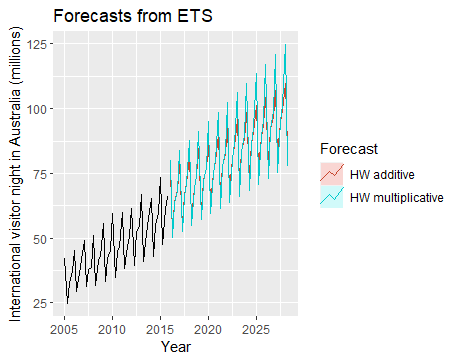
这两种方法具体数学上的区别,这里我们不做探讨,而仅关注应用层面的区别。一般来说,下图中左侧类型的数据适合用累加法,右侧的适合用累乘法。
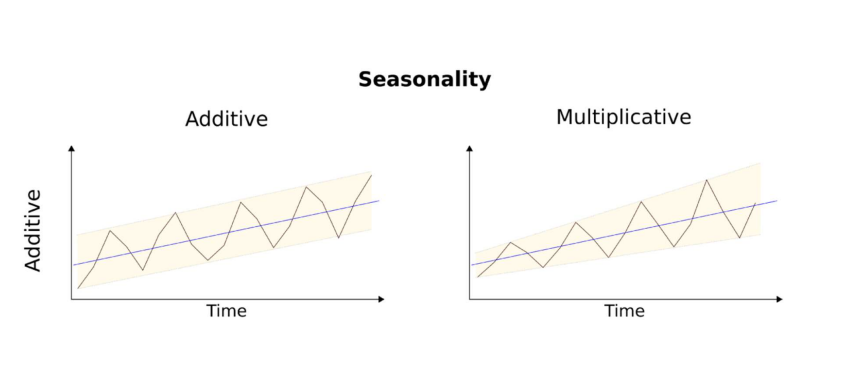
霍尔特-温特斯阻尼法(Holt-Winters’ Additive Method)
阻尼法的方程形式如下:
| Forecast | $\hat{y}{T+h \mid T}=(l{T}+(\phi +\phi^2 +…+\phi^{h})b_{T})s_{T+h-m(k+1)}$ |
|---|---|
| Level | $l_{T}= \alpha \frac{y_{T}}{s_{T-m}}+(1-\alpha)(l_{T-1}+\phi b_{T-1})$ |
| Tred | $b_{T}=\beta (l_{T}-l{T-1})+(1- \beta)\phi b_{T-1}$ |
| Seasonal | $s_{T}=\gamma \frac{y_{T}}{(l_{T-1}-\phi b_{T-1})}+(1-\gamma)s_{T-m}$ |
使用方法及对比:
1 | autoplot(a10) |
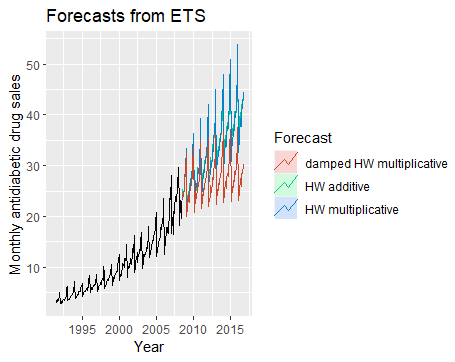
ETS模型
ETS模型是一个时间序列模型系列,其基础状态空间模型由水平分量、误差项(E)、趋势分量(T)、和季节分量(S)组成。
其中:
误差项(Error)包含加性(A)、乘性(M)
趋势分量包含普通(N)、加性(A)、阻尼加性(Ad)、乘性(M)、阻尼乘性(Md)
季节分量普通(N)、加性(A)、乘性(M)
- ETS(Error, Trend, Seasonal):
- Error = {A, M}
- Trend = {N, A, M, Md}
- Seasonal = {N, A, M}
如趋势项,其包含level、growth两部分,共有五种:
| Type | Form |
|---|---|
| None: | $T_{h} = l$ |
| Additive: | $T_{h} = l+bh$ |
| Additive Damped: | $T_{h} = l+(\phi +\phi^2 +…+\phi^{h})b$ |
| Multiplicative: | $T_{h} = lb^h$ |
| Multiplicative Damped: | $T_{h} = lb^{(\phi +\phi^2 +…+\phi^{h})}$ |
将E、T、S组合在一起,可知共有30种ETS模型。
例如:
A,N,N 模型代表有着加性误差项的一次指数平滑模型;
A,A,N 模型代表有着加性误差项的Holt平滑模型;
M,A,M 模型代表有着乘性误差项的Holt-Winters’平滑模型;
使用方法:
1 | ### ets方程会自动输出适合输入数据的ETS模型 |
这里需要注意的是,由于使用乘性趋势会使模型生成速度减缓,因此默认中,ets函数不开启乘性趋势,我们需手动将其设置打开:
1 | ets(h02, allow.multiplicative.trend=TRUE) |
通过pipeline直接生成预测:
1 | h02 %>% ets() %>% forecast() %>% autoplot() |
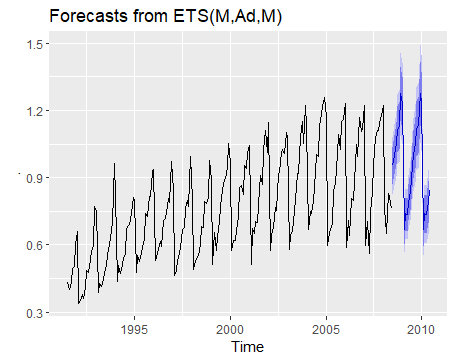
通过test数据测试效果:
1 | train <- window(h02, end=c(2006,6)) |
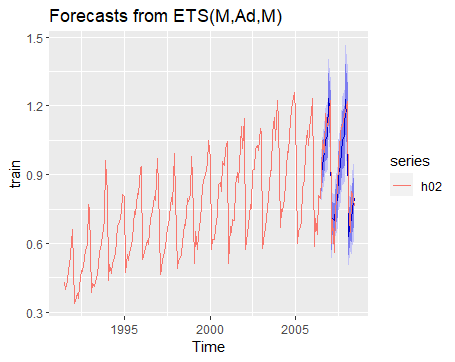
虽然有自动化函数,但如果我们想人工查验一下数据的各项特征,则可以使用下述代码:
1 | autoplot(mstl(h02)) |
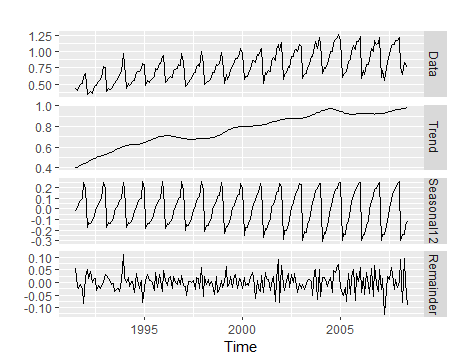
便可看出原数据的趋势、误差及季节性特征,对于上图的数据,则应使用ETS[MAM]模型。
额外参考资料:Forecasting with Exponential Smoothing: The State Space Approach
整合移动平均自回归模型(ARIMA)
平稳性及差分(Stationarity and Differencing)
平稳性(Stationarity)
平稳性指对于一个时间序列,时间因素对于数据本身没有影响。
平稳时间序列有下述特征:
大致水平、方差恒定、没有长期显著的可预测特征
如何鉴别平稳化:
- 观察时序图特征
- 平稳时序的ACF较快降至零
- 非平稳时序的ACF下降较慢
- 非平稳时序的r1一般较大且为正
差分(Differencing)
前文我们有提到将数据方差平稳化的方式,而为了让数据整体平稳,我们还需要将均值平稳化,这就需要用到差分。
差分的意思是将当期数据减上期数据,操作很简单。
对于季节性数据,则是将当季数据减上季数据。
单位根检验(Unit Root Tests)
这是用来检验平稳性的一种统计检验法,本课中我们讲到的是KPSS检验(Kwiatkowski-Phillips-Schmidt-Shin Test)
它的零假设是:原数据为平稳且非季节性。(检验值小于显著值表示平稳)
类似的还有ADF检验(Augmented Dickey–Fuller Test)
例:
1 | library(urca) |
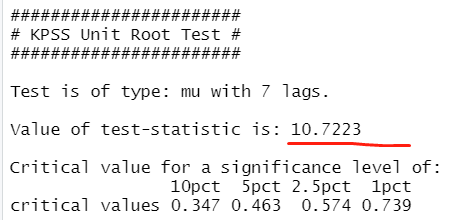
这里的检验值为10.7,大于显著值,表示拒绝原假设,即数据为非平稳。
让我们对数据进行一定平稳化处理:
1 | goog %>% diff() %>% ur.kpss() %>% summary() |
这里我们首先进行了差分,然后再进行检验,可得:
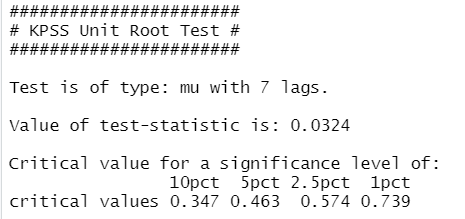
可见检验值低于显著值,则处理后的数据为平稳时序。
ndiff函数可以告诉我们使数据稳定所需要的差分次数:
1 | ndiffs(goog) |
nsdiff函数则是用来得到季节性数据的差分次数,组合使用:
1 | autoplot(usmelec) |
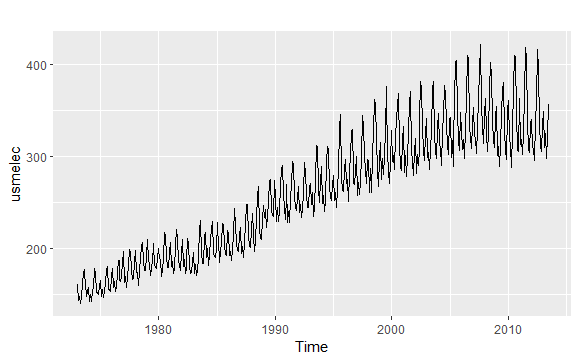
1 | usmelec %>% log() %>% nsdiffs() |
得到返还值:1,于是进行一次季节性差分:
1 | usmelec %>% log() %>% diff(lag=12) %>% ndiffs() |
得到返还值:1,于是再进行一次普通差分:
1 | usmelec %>% log() %>% diff(lag=12) %>% diff(lag=1) %>% ndiffs() |
处理后的数据样貌:
1 | usmelec %>% log() %>% diff(lag=12) %>% diff(lag=1) %>% autoplot() |
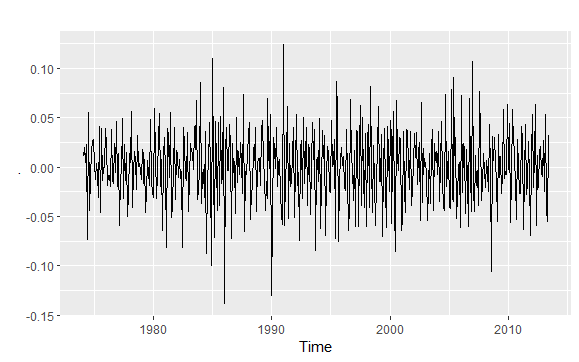
KPSS检验:
1 | usmelec %>% log() %>% diff(lag=12) %>% diff(lag=1) %>% ur.kpss() %>% summary() |
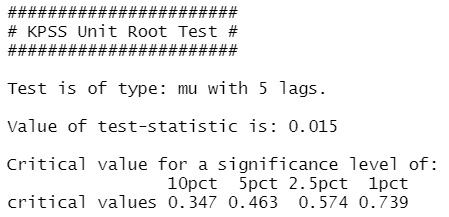
成功转换为平稳时序。
非季节性ARIMA模型(Non-seasonal ARIMA model)
自回归模型AR(Autoregressive Model)
自回归方法的优点是所需资料不多,可用自身变数数列来进行预测。但是这种方法受到一定的限制:
必须具有自相关,自相关系数()是关键。如果自相关系数($R$)小于0.5,则不宜采用,否则预测结果极不准确。
代码模拟:
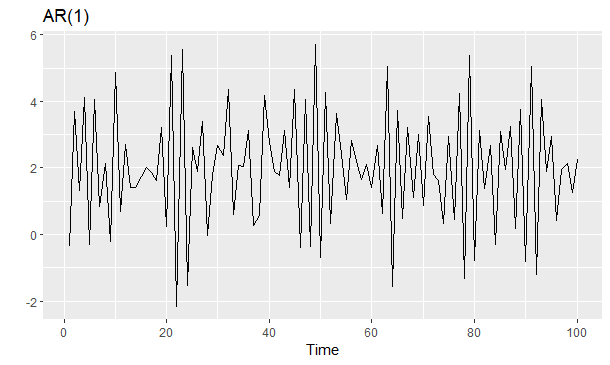
1 | ar1 <- 2 + arima.sim(list(ar = -0.8), n = 100) |
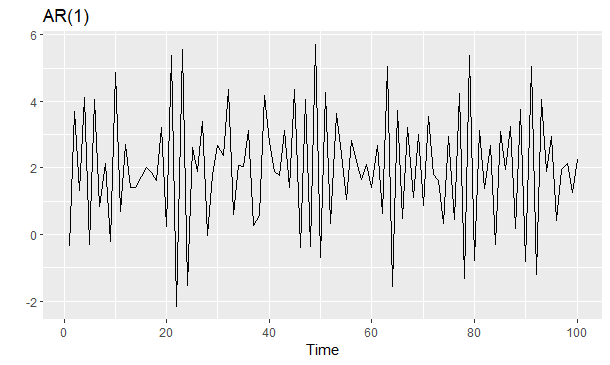
移动平均模型MA(Moving Average Model)
MA模型和AR大同小异,它并非是历史时序值的线性组合而是历史白噪声的线性组合。与AR最大的不同之处在于,AR模型中历史白噪声的影响是间接影响当前预测值的(通过影响历史时序值)。
代码模拟:
1 | set.seed(2) |
移动平均自回归模型ARMA(Autoregressive Moving Average Model)
将AR和MA模型混合可得到ARMA模型,AR(p)和MA(q)共同组成了ARMA(p,q)。下面模拟一个ARMA(1,1)序列:
1 | x <- arima.sim(n=1000, model=list(ar=0.5, ma=-0.5)) |
那么在建模过程中应该如何选择ARMA模型的最佳参数p和q呢?最常用的技术是采用循环在p和q各自0到5(或者更大)的范围内搜索最小AIC或BIC的(p,q)组合。
整合移动平均自回归模型(ARIMA)
终于,把上述的几个模型都组合在一块,就得到了这个名字看上去很高级的ARIMA模型。
ARIMA模型是在ARMA模型的基础上解决非平稳序列的模型,因此在模型中会对原序列进行差分。
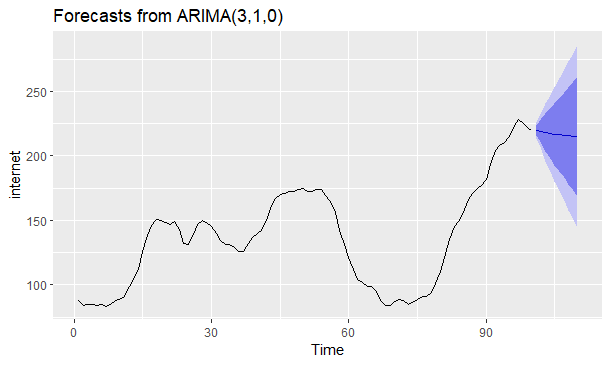
例:对internet数据集预测
1 | ggtsdisplay(internet) |
SARIMA、动态回归及其他高级预测模型
在前文的基础上,ARIMA还可以引入季节性因素,组建成季节性(S)ARIMA,也有其它的模型,如动态回归、神经网络模型等等,然而,时间有限,这节课没有详述这些内容,因此,本学渣也没去做太多拓展阅读,实在是太累了。不过未来闲着的时候,我可能还是会去研究下吧,这里先挖个坑。
后记
至此,这一学期的时序分析课程笔记就算是整理完毕了。回过头来看,这门课的笔记洋洋洒洒写了快一万来字,虽然本人文笔实在很拙劣,但是码了这么多字多少也还是挺有成就感的。当然,眼尖的同学其实能看出来,学到ARIMA时本人学得就不是很扎实了,笔记也记得不是很能让人看明白。不过不管怎样,期末考试和Presentation还是搞定了,暂时就不再花更多时间去研究了,毕竟还有其他课程和项目要做。
写到此处,不免有些感慨,为什么呢,主要是因为自己已经很多年没有这么高强度地学习了,就这两篇的笔记所涉及到的内容,是仅在半学期的两学分课程中讲完的,而与国内的大多大学不同,本学渣所在的Santa Clara University采取的是Quarter制,也就是三个月一学期,一年3学期。这就是说,博客里两篇时序分析学习笔记中的内容,仅用了一个半月就学习完毕,这就意味着本人前两个月几乎每天都在高强度地读材料、看讲义、写作业,可能对于很多一直努力的大佬来说,这也没什么,但对于摸了一辈子鱼的本人来说,属实是高压生活了(想学东西,果然在哪里都是不能避开填鸭式这条道路的)。
不论如何,这门课也算是收获颇丰,这篇博文也就来到了尾声。本人不擅长、也不喜欢拽文,就不多说什么矫情的话了,如果真的有什么人有够闲,看到了这里,那也算是缘分了,很感谢。当然还是要说,本人同时深感抱歉,浪费了你人生宝贵的时间。
Anyway,就让我们在别的什么地方再见吧。
<br>
于2022年5月3日完结