时间序列案例分析（一） —— Lac Leman Festival De La Musique

发表于 更新于 分类于 阅读次数： 本文字数： 3.8k 阅读时长 ≈ 3 分钟

banner

前言

在本周的时序分析课程中，我们主要对一个音乐会案例进行了分析，该案例数学层面的难度虽然不太大，不过用到的一些方法值得记录。

该案例名为“Lac Leman Festival De La Musique”，其主要模拟了我们作为一场音乐会的管理人员，该如何制定音乐会的周边销售计划。

案例场景概述(Senario Description)

案例原文件可以在此购买：

Lac Leman Festival de la Musique (A)

Lac Leman Festival de la Musique (B)

该案例的原文件文字冗长，明明是个商业案例，却时常不合时宜的使用修辞来描述人物心情，读之尴尬，故本人在此简单概括下核心需要使用的内容：

假设我们的音乐会分别有周五、周六两天的、内容不同的场次。我们作为主办方，想要将周五当天的表演录制为DVD，进而在周六的场次贩卖录制好的光盘。（这里设定为我们只拿到了周六当天售卖的版权，周六过后所有未销售的光盘全部需要销毁）

而进行DVD录制分别有下述成本：

  1. 雇佣录制团队 11740CHF
  2. 烧录母碟 3000CHF
  3. 光碟量产开机费 1250CHF
  4. 光碟量产费：
    如果制作量小于等于5300张，则每张光盘0.86CHF
    如果制作量大于5300张，超出的部分每张加收0.2CHF
  5. 版税(Royalty) 每张1.02CHF（仅包含卖出的，烧录但未卖出的不算）

最终每张DVD所定的售价为：18CHF

可以看出，由于制作产品本身需要成本，且有意愿购买DVD的人数不确定，因此无论做的太少或太多都会有损失风险，此时我们便需要对各类因素做预测，以计算出最优的制作数量。

问题一：根据给定条件求利润

在这一问题中，案例假定我们已经得到了下述数据，需要我们在这些条件下计算出卖DVD的所得利润。

  1. 周六的参加人数为 24139
  2. 18.92% 的参加者会购买DVD
  3. 我们烧录了4500份DVD

逻辑上来说，本题很简单，只需套入条件，算出上文中的成本，然后用收益减成本即可，然而，为了后续问题（主要是5、6两题）的可计算，本题构建一个利润方程来求解：

1
2
3
4
5
6
7
8
9
10
11
12
13
profitf <- function (People, Total) {
  Revenue <- 18 * min(People, Total)
  if (Total > 5300) {
    cost <- 0.86 * Total + (0.86 + 0.2) * (Total - 5300)
  }
  else {
    cost <- 0.86 * Total
  }
  Royalty <- 1.02 * Total
  totalCost <- 15990 + cost + Royalty
  Profit <- Revenue - TotalCost
  return(Profit)
}

两项输入中，People为购买DVD的人数，Total为总生产的DVD数量。

构建好方程后，本题便只需调用即可：

1
profitf(24139*0.1892, 4500)

得到解为：56550CHF

问题二：基于往年数据，简单预测今年数据

这一题中，案例给出了往年的周六参加人数的数据：

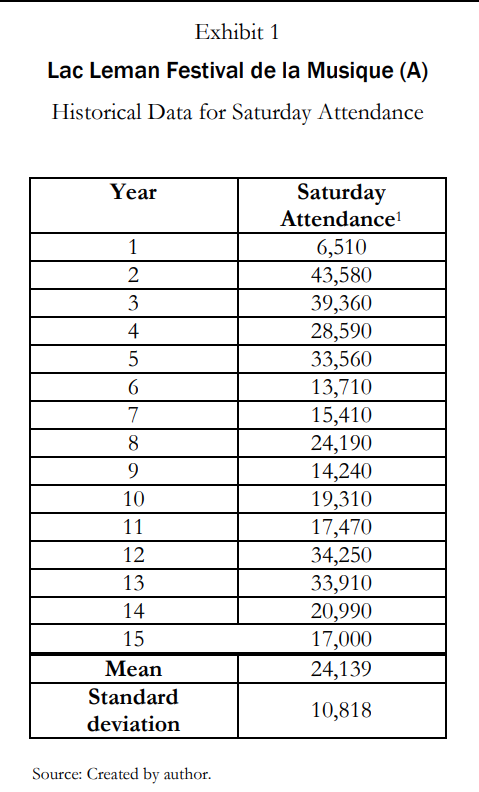
首先我们绘制下该数据随时间变化的图：

1
2
3
autoplot(data.ts) +
  ggtitle("Attendance") +
  xlab("Year") + ylab("Saturday Attendance")

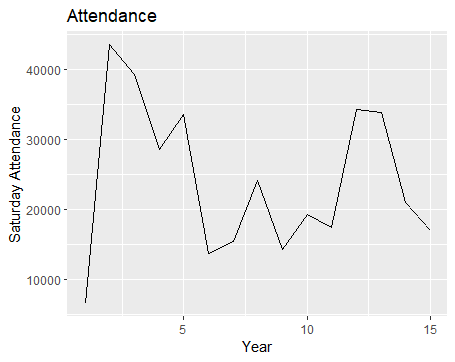
坦白来说，这个数据具备白噪音特征，不适合预测，然而，这里仅当练手，便无所谓了，先把方法套上去再说。

通过观测可知其没有季节性(Seasonal)特征，所以我们便不采用季节法预测，而是采用平均、朴素、和漂移法：

1
2
3
4
5
6
7
8
autoplot(data.ts) +
  ggtitle("Attendance") +
  xlab("Year") + ylab("Saturday Attendance") +
  autolayer(meanf(data.ts, h = 1), PI = FALSE, series = "Mean") +
  autolayer(naive(data.ts, h = 1), PI = FALSE, series = "Naïve") +
  autolayer(rwf(data.ts, drift = TRUE, h = 1),
            PI = FALSE,
            series = "Drift")

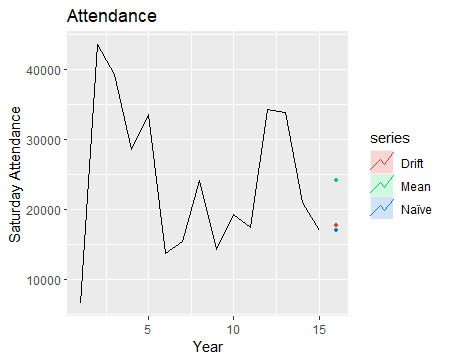
这样我们便得到了三个预测值

问题三：样本标准差

该问题需要我们基于已有信息求出样本平均方差。

假设我们得到了周六参加音乐会的人数预测值，我们此时其实还是无法确定该生产多少DVD，因为参与音乐会的人不一定买DVD。于是，我们就需要知道参加音乐会的有多少人愿意购买DVD。

在案例中，主办方向以往参与过的客户发送了调查问卷邮件，以询问其是否愿意购买DVD。共计发放150封问卷，收到37封反馈，其中8封表示愿意购买。

于是，基于此，我们便可以假定每个观众购买DVD的概率均值$p$为$8/37=0.1892$

而由于这是一个二项分布问题，标准差计算公式为：$\sqrt{(p(1-p))}=0.3917$，进而样本标准差即可求出为：$\sqrt{((p(1-p))/37)}=0.06439508$

问题四：增加自变量，进行回归分析预测

在这一问题中，案例引入了三个新数据：周五观众人数、周五是否下雨、周六是否下雨。

同时，我们已知今年周五的观众人数为：18394，且今年周五没有下雨。案例要求我们基于上述条件，进行今年周六的观众人数预测.

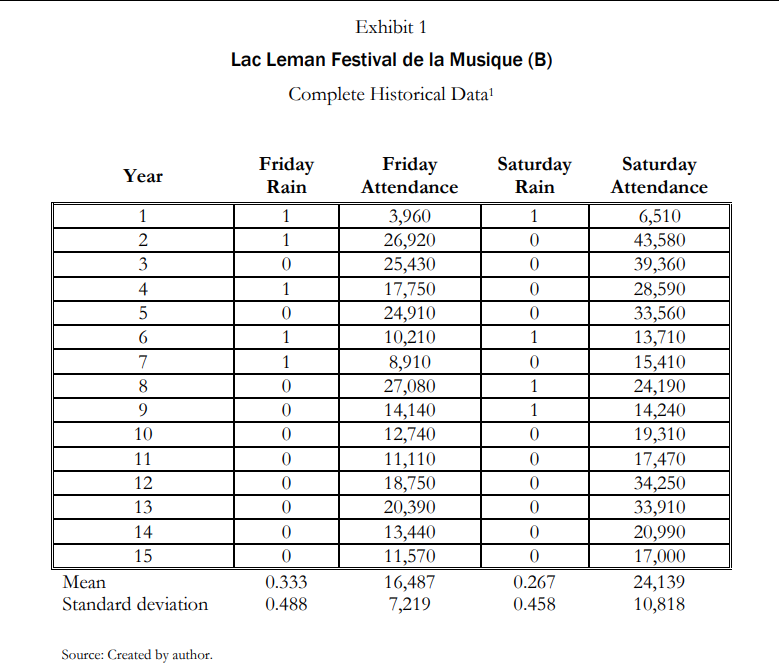
引入上述数据作为自变量，我们便可以进行时序回归：

1
2
fit = tslm(SatAtt ~  rain6 + FriAtt + rain5, data = all)
summary(fit)

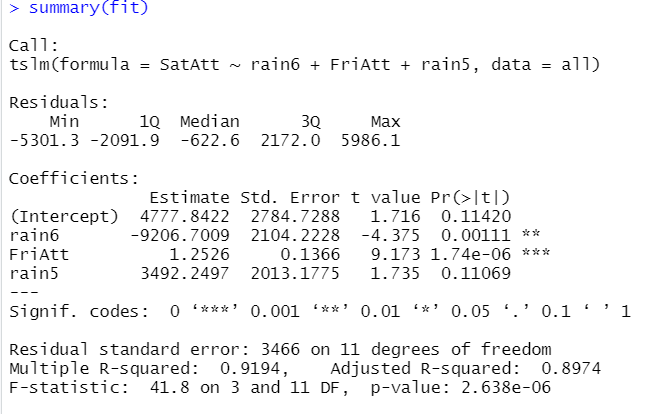
得到回归模型后，我们便可以输入自变量的未来值来预测，而此时，今年周六是否有雨仍未未知，因此我们进行分类讨论：

  1. 假设周六无雨：
1
2
3
4
5
newdata1 <- data.frame(rain5 = 0,
                       FriAtt = 18394,
                       rain6 = 0)
fcast1 <- forecast(fit, newdata = newdata1)	
autoplot(fcast1)
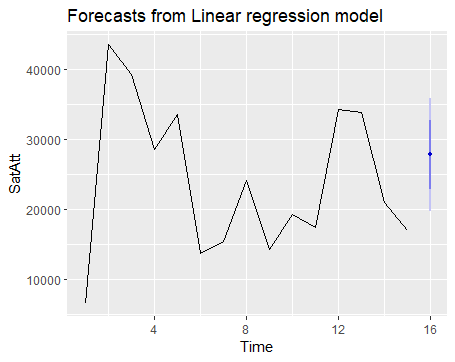
  1. 假设周六有雨：
1
2
3
4
5
newdata2 <- data.frame(rain5 = 0,
                       FriAtt = 18394,
                       rain6 = 1)
fcast1 <- forecast(fit, newdata = newdata2)	
autoplot(fcast2)

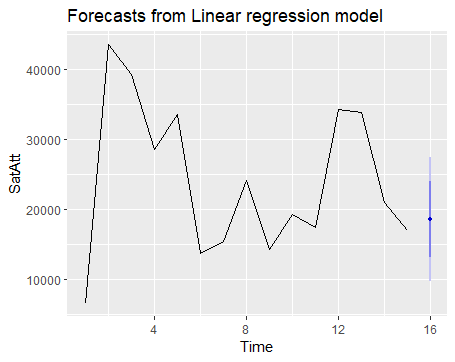
问题五：基于给定条件，求风险分布

在这一问题中，进一步的，我们假设周六下雨的概率为80%，且我们制作了4500张DVD，案例要求我们找到利润的分布

在这一问题中，我们用到了蒙特卡洛模拟(Monte Carlo Simulation)，由于所需的概率分布都已知，我们可以使用模拟出的数据，来计算利润，并绘制分布图。

1
2
3
4
5
6
7
8
9
set.seed(123)

n1 <- 2500
a <- rnorm(n1, 18611, 3466)  # attendance with rain
b <- rnorm(n1, 27818, 3466)  # attendance with no rain
c <- rbinom(n1, 1, 0.8)

attendance6 = c * a + (1-c) * b
hist(attendance6, breaks=50)

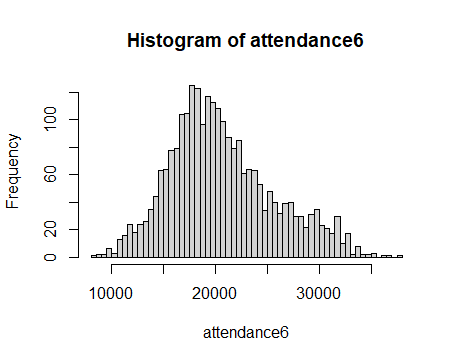
此时，我们便得到了模拟出的周六观众分布图。

接下来，我们将每一个模拟的观众数据代入第一题中的收益方程，便可得到利润分布：

1
2
3
4
5
6
7
8
9
10
11
12
pf <- numeric(length = length(f))
pfneg <- numeric(length = length(f))
for(i in 1:length(f)) {
  pf[i] <- profitf((f[i],4500)
  if (pf[i]<0) {
    pfneg[i]=1
  }
  else {
    pfneg[i]=0
  }
}
hist(pf, breaks=50)

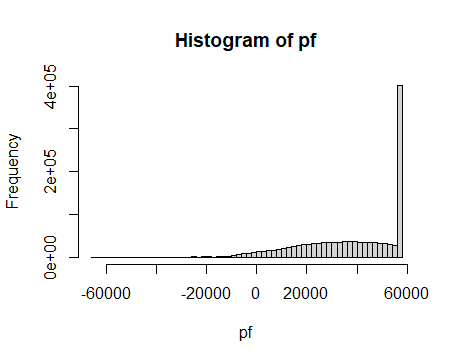
其中，pfneg表示负利润，也就是亏损

1
mean(pfneg)

最后我们求其均值，便可以得到亏损概率为0.0390864。

p.s. pfneg并非题目所要求，只是为了结果更易读而存在。

问题六：DVD生产建议

这一题中，所有已知条件都与上一题一致，除了生产DVD数目不再提供，案例要求我们给出推荐的DVD生产数量。

主要思路和穷举法相似，将一定区间的数字输入收益函数中循环，然后取收益最高的点：

1
2
3
4
5
6
7
8
9
10
11
12
13
dvd <- 4500+25*c(0:100)
profit <- numeric(length = length(dvd))

for(j in 1:length(dvd)) {
  for(i in 1:length(f)) {
    pf[i] <- profitf(f[i],dvd[j])
  }
  profit[j] <- mean(pf)
}

dvdprofit <- cbind(dvd,profit)
dvdprofit
plot(x=dvd,y=profit)

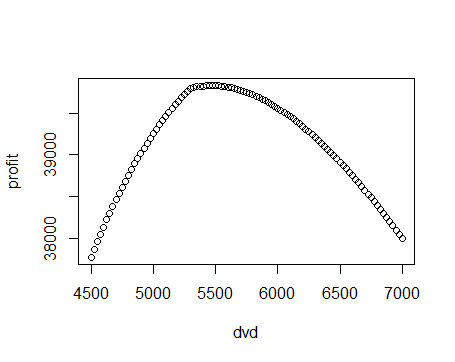
直观的可以看出，生产量5500左右的利润最大。