机器学习期末Kaggle项目实践 —— House Prices - Advanced Regression Techniques

发表于 更新于 分类于 阅读次数： 本文字数： 29k 阅读时长 ≈ 27 分钟

banner

前言

如果有关注本人近期的博文，就知道本学渣最近在啃机器学习这门课程，这门课显然对于本人这种文科生来说有些太硬了，但无论如何，通过忽略不少的底层数学原理及推导，这几个月也算跌跌撞撞学下来了。

不知不觉，也就到了本学期的末尾，本人自然便要面对这门课的期末考试，而教授将我们的期末分为了两部分：笔试和比赛。笔试部分这里就不多提了，主要就是考察之前三篇笔记中的所有概念，而期末的另一部分，则是到Kaggle上打比赛，最终成绩根据排名给出。本学期给我们分配到的比赛为：House Prices - Advanced Regression Techniques ，主要内容是根据特征数据，建模并预测某地的房价走势。

由于本人智力水平一般，再加上这门课的速度实在是太快，因此时常会忘记某些概念和用法。故而在此开一篇文章，单独记录下课程期末项目中每一步的思路，以使整体框架逻辑清晰。

同时，鉴于本人只是初学者入门水平，文中的方法难免存在各种问题，如果有大佬发现任何值得改进的地方，务必在评论区不吝指教，本人将感激不尽！

文中的所有代码已经托管到了我的Github仓库，可以在这里找到：Kaggle House Price Competition

解释性数据分析(Explotory Data Analysis)

EDA这一部分，实在是有点鸡肋，做了没什么大用，但不做又感觉少了点什么……

原数据概况

首先我们读取数据集

1
2
3
4
import pandas as pd 
pd.set_option('display.max_columns', 500)
test_raw = pd.read_csv("input/test.csv")
train_raw = pd.read_csv("input/train.csv")

通过观察列名，可知其中有一行Id列，对于预测没有用处，我们首先删去这一列，同时要备份留作后用。

1
2
3
4
5
6
7
# Backup
train_ID = train_raw['Id']
test_ID = test_raw['Id']

# Drop
train_raw.drop("Id", axis = 1, inplace = True)
test_raw.drop("Id", axis = 1, inplace = True)

这之后，训练集变为80列，测试集变为79列，多出来的一列为需要预测的SalePrice。

1
2
3
4
5
train_raw.shape
# (1460, 80)

test_raw.shape
# (1459, 79)

特征概况

原始数据中，特征分为分类数据和数字数据。

分别获取列名：

1
2
categoricalColumns = train_raw.select_dtypes(include=['object']).columns.to_list()
numericalColumns = train_raw._get_numeric_data().columns.to_list()

对于分类特征，原始数据中有43列：

1
2
3
4
train_cat_raw = train_raw[categoricalColumns]
train_cat_raw

# 1460 rows × 43 columns

对于数字特征，原始数据中有37列：

1
2
3
4
train_num_raw = train_raw[numericalColumns]
train_num_raw

# 1460 rows × 37 columns

目标概况

首先我们获取目标数据：

1
2
target = "SalePrice"
y_train_raw = train_raw[target]

对其进行一些简单可视化：

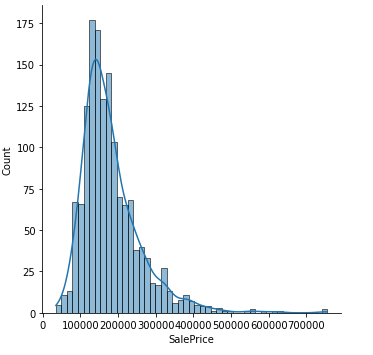
1
2
3
4
import seaborn as sns
from matplotlib.pyplot import figure
figure(figsize=(5, 10))
sns.boxplot(data = y_train_raw)

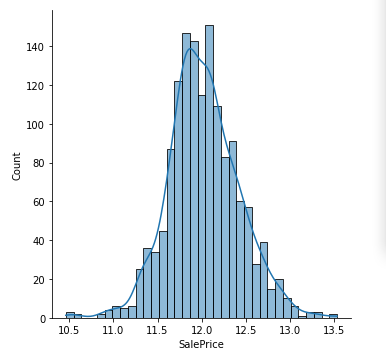
可见其并非正态分布，而对于线性模型而言，需要数据符合正态分布，于是我们对其对数化：

1
sns.displot(data = np.log1p(y_train_raw), kde=True)

将其存入y_train

1
y_train = np.log1p(y_train_raw)

然后观察变量间的相关性：

1
2
3
4
5
6
7
8
import seaborn as sns
import matplotlib.pylab as plt
from matplotlib.pyplot import figure
%matplotlib inline
figure(figsize=(30, 15))
mask = np.triu(np.ones_like(train_num_raw.corr(), dtype=bool))
heatmap1 = sns.heatmap(train_num_raw.corr(), vmin=-1, vmax=1, annot=True, cmap='BrBG', mask=mask)
heatmap1.set_title('Train Column Correlation Heatmap', fontdict={'fontsize':18}, pad=16)

图的体积比较大，就不在这里截图了，可以到我的Github上查看详细的图，不过其实这一步没有什么用。

数据清洗与填补

不难发现，这一数据集存在较多空值，在这一章节，我们对数据集中的空值进行统一处理。

首先为了减少工作量，我们合并训练、测试集：

1
all_raw = pd.concat((train_raw.drop(target, axis=1), test_raw), ignore_index=True)

之后凡是不会涉及到数据溢出的填补操作，我们都在all_raw之上进行。

单一数据列处理

当某列特征的数据几乎完全只有一个值时，我们可以认为这列对于模型没有贡献，因此对其进行删除操作。

这里本人采用的判断标准是：如果某列的某个值占比超过了该列的99%，则判定该列为单一数据列。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
# If a value accounts for more than 99% of one column, we define the column as single value column, and we can drop it.

singleValueColumns = []

for i in all_raw.columns.unique().tolist():
    if all_raw[i].value_counts(normalize=True).iloc[0] > 0.99:
        singleValueColumns.append(i)

# Show single valew columns
singleValueColumns

# 输出：
# ['Street', 'Utilities', 'PoolArea']

接下来只需将上述列删除即完成这一步的处理。

1
all_raw = all_raw.drop(singleValueColumns, axis=1)

类别数据处理

对于类别数据，由于网站提供的数据描述文件中提供了一部分的特征为Na的解释，我们将其直接应用，而对于没有提供描述的，我们基于常识做一些假设，将Na填补为已有数据，具体的假设可以在我托管在Github上的源代码中找到。

总之我们建立一个这样的填补索引列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# Make Na conversion list

cat_na_conversion = [("MasVnrType", "None"),
                     ("BsmtQual", "None"), 
                     ("Electrical", "SBrkr"),
                     ("BsmtCond", "None"),
                     ("BsmtExposure", "None"),
                     ("BsmtFinType1", "None"),
                     ("BsmtFinType2", "None"),
                     ("CentralAir", "N"),
                     ("Condition1", "Norm"), 
                     ("Condition2", "Norm"),
                     ("ExterCond", "TA"),
                     ("ExterQual", "TA"), 
                     ("FireplaceQu", "None"),
                     ("GarageType", "None"), 
                     ("GarageFinish", "None"), 
                     ("GarageQual", "None"), 
                     ("GarageCond", "None"), 
                     ("HeatingQC", "TA"), 
                     ("KitchenQual", "TA"), 
                     ("Functional", "Typ"), 
                     ("MSZoning", "None"),
                     ("Exterior1st", "VinylSd"), 
                     ("Exterior2nd", "VinylSd"), 
                     ("SaleType", "WD"),
                     ("PoolQC", "None"),
                     ("Fence", "None"),
                     ("MiscFeature", "None"),
                     ("Alley", "None")]

然后进行遍历列名的填补：

1
2
for colName, toStr in cat_na_conversion:
    all_raw.loc[:, colName] = all_raw.loc[:, colName].fillna(toStr)

数字数据处理

首先我们筛选出所有的需要处理的列名：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Find numerical colimns with missing values

num_na_col = all_raw.columns[all_raw.isna().any()].tolist()
num_na_col

#['LotFrontage',
#  'MasVnrArea',
#  'BsmtFinSF1',
#  'BsmtFinSF2',
#  'BsmtUnfSF',
#  'TotalBsmtSF',
#  'BsmtFullBath',
#  'BsmtHalfBath',
#  'GarageYrBlt',
#  'GarageCars',
#  'GarageArea']

其中，除了'LotFrontage'一列外，其余的其实都和我们上一步填补的分类特征相关，我们也可以做相同的假设，将其中所有的Na填补为0

1
2
3
4
5
6
7
8
9
10
num_to_zero_col = num_na_col.copy()
num_to_zero_col.remove('LotFrontage')
num_to_zero_col

for col in num_to_zero_col:
    all_raw[col] = all_raw[col].fillna(0)

all_raw.columns[all_raw.isna().any()].tolist()

# ['LotFrontage']

处理完后仅剩'LotFrontage'一列存在空值，我们接下来对其进行处理：

这里也用了一个假设，我们认为处于同一个Neighbor下的房子有相似的LotFrontage值，所以我们可以先以Neighbor归类，然后用中位数填补。

但这里如果直接用all_raw来做处理，我们会将训练集的数据填到测试集中，这会导致数据泄露，因此我们首先将其重新分为两部分：

1
2
3
4
5
train_imputed["LotFrontage"] = train_raw_Lot.groupby("Neighborhood")["LotFrontage"].transform(
    lambda x: x.fillna(x.median()))

test_imputed["LotFrontage"] = test_raw_Lot.groupby("Neighborhood")["LotFrontage"].transform(
    lambda x: x.fillna(x.median()))

此时我们便得到了填补后的数据，可见其不再有空值：

1
2
3
4
5
6
7
train_imputed.isna().sum().max()

# 0 

test_imputed.isna().sum().max()

# 0

特征工程

预处理

我们留意到：对于原数据中的某些数字特征，其实际表示的却是分类（如建造年份），而分类数据也同理，因此我们考虑将这些特征转换为其实际对应的格式。

有分类特征的数字列名为：

YrSold MoSold GarageYrBlt MSSubClass OverallCond YearBuilt

这里为了方便处理，我们还是将其合并为整表：

1
2
3
# .loc[:len(train_raw)-1, :]
# .loc[len(test_raw)+1:, :]
all_imputed = pd.concat((train_imputed, test_imputed), ignore_index=True)

然后将上述列进行转换：

1
2
3
4
num_to_cat_list = ["GarageYrBlt", "MSSubClass", "OverallCond", "YrSold", "MoSold", "YearBuilt", "YearRemodAdd"]

for i in num_to_cat_list:
    all_imputed[i] = all_imputed[i].astype(str)

同时，我在网上看到其它的一些大佬对于某些原始列进行运算，以制造新特征，我觉得挺有道理，就复刻了一些过来：

1
2
3
4
5
6
7
8
9
10
11
all_imputed['TotalArea'] = all_imputed['TotalBsmtSF'] + all_imputed['1stFlrSF'] + all_imputed['2ndFlrSF']

all_imputed['TotalBath'] = (all_imputed['FullBath'] + (0.5 * all_imputed['HalfBath']) +
                               all_imputed['BsmtFullBath'] + (0.5 * all_imputed['BsmtHalfBath']))
all_imputed['TotalBsmtbath'] = all_imputed['BsmtFullBath'] + (0.5 * all_imputed['BsmtHalfBath'])


all_imputed['TotalPorchSF'] = (all_imputed['OpenPorchSF'] + all_imputed['3SsnPorch'] +
                            all_imputed['EnclosedPorch'] + all_imputed['ScreenPorch'] + all_imputed['WoodDeckSF'])

allData = all_imputed.drop(['TotalBsmtSF', '1stFlrSF', '2ndFlrSF', 'FullBath', 'HalfBath', 'BsmtFullBath', 'BsmtHalfBath', 'OpenPorchSF', '3SsnPorch', 'EnclosedPorch', 'ScreenPorch', 'WoodDeckSF'])

然后我们便可以拿到预处理后的训练+测试集：

1
2
X_train = allData.loc[:len(train_raw)-1, :]
X_test = allData.loc[len(test_raw)+1:, :]

类别特征工程

获取所有的类别列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
cat_features = allData.select_dtypes(include=['object']).columns.to_list()

# ['MSSubClass',
#  'MSZoning',
#  'Alley',
#  'LotShape',
#  'LandContour',
#  'LotConfig',
#  'LandSlope',
#  'Neighborhood',
#  'Condition1',
#  'Condition2',
#  'BldgType',
#  'HouseStyle',
#  'OverallCond',
#  'YearBuilt',
#  'RoofStyle',
#  'RoofMatl',
#  'Exterior1st',
#  'Exterior2nd',
#  'MasVnrType',
#  'ExterQual',
#  'ExterCond',
#  'Foundation',
#  'BsmtQual',
#  'BsmtCond',
#  'BsmtExposure',
#  'BsmtFinType1',
#  'BsmtFinType2',
#  'Heating',
#  'HeatingQC',
#  'CentralAir',
#  'Electrical',
#  'KitchenQual',
#  'Functional',
#  'FireplaceQu',
#  'GarageType',
#  'GarageYrBlt',
#  'GarageFinish',
#  'GarageQual',
#  'GarageCond',
#  'PavedDrive',
#  'PoolQC',
#  'Fence',
#  'MiscFeature',
#  'MoSold',
#  'YrSold',
#  'SaleType',
#  'SaleCondition']

对于其中的某些没有很多不同数据的列，我们可以简单的使用独热编码，因为这些列不会造成过大的稀疏矩阵，对于其中的表示大小的分类，我们考虑使用顺序编码，而剩下来的所有列，我们用目标编码。首先我们筛选出这些列：

1
2
3
4
5
6
ordinal_cat_features = ['FireplaceQu', 'BsmtQual', 'BsmtCond', 'GarageQual', 'GarageCond', 'ExterQual', 'ExterCond', 'HeatingQC', 'PoolQC', 'KitchenQual', 'BsmtFinType1',
                        'BsmtFinType2', 'Functional', 'Fence', 'BsmtExposure', 'GarageFinish', 'LandSlope', 'LotShape', 'MSSubClass', 'OverallCond', "YrSold", "MoSold", "YearBuilt", "YearRemodAdd"]

onehot_cat_features = ['CentralAir', 'PavedDrive']

target_cat_features = list(set(cat_features) - set(ordinal_cat_features) - set(onehot_cat_features))

有了列表以后，我们便可以在之后用列转换来处理。

P.S. 后来的调教中，我发现顺序编码效果一般，于是后来就只用了独热和目标编码。

数字特征工程

获取所有数字列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
num_features = allData._get_numeric_data().columns.to_list()

# ['LotFrontage',
#  'LotArea',
#  'OverallQual',
#  'MasVnrArea',
#  'BsmtFinSF1',
#  'BsmtFinSF2',
#  'BsmtUnfSF',
#  'LowQualFinSF',
#  'GrLivArea',
#  'BedroomAbvGr',
#  'KitchenAbvGr',
#  'TotRmsAbvGrd',
#  'Fireplaces',
#  'GarageCars',
#  'GarageArea',
#  'MiscVal',
#  'TotalArea',
#  'TotalBath',
#  'TotalBsmtbath',
#  'TotalPorchSF']

这里也可以看一下数字列与目标列的相关度：

1
2
3
4
5
6
7
8
9
pd.concat([X_train[num_features], y_train], axis=1)
import seaborn as sns
import matplotlib.pylab as plt
from matplotlib.pyplot import figure
%matplotlib inline
figure(figsize=(30, 15))
mask = np.triu(np.ones_like(pd.concat([X_train[num_features], y_train], axis=1).corr(), dtype=bool))
heatmap1 = sns.heatmap(pd.concat([X_train[num_features], y_train], axis=1).corr(), vmin=-1, vmax=1, annot=True, cmap='BrBG', mask=mask)
heatmap1.set_title('Train Column Correlation Heatmap', fontdict={'fontsize':18}, pad=16)

也不截图了，可以到我的Github上看，总之就是相关性都挺高的。

主成分分析(PCA)

考虑对原数据进行PCA降维：

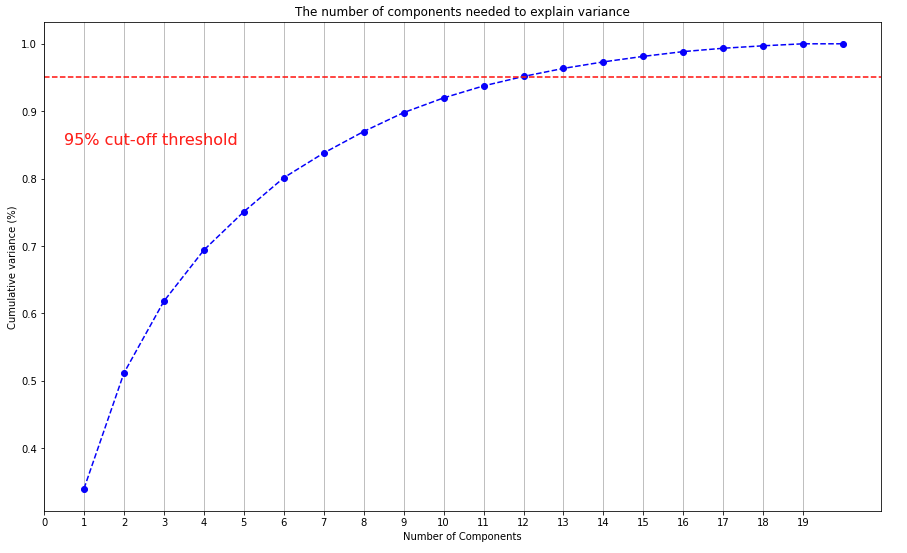
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import MinMaxScaler

pca_scaled = make_pipeline(RobustScaler(), 
                           MinMaxScaler(),
                           PCA(n_components=len(num_features)))

X_pca_scaled = pca_scaled.fit_transform(X_train[num_features])

xi = np.arange(1, len(num_features)+1, step=1)
y = np.cumsum(pca_scaled.named_steps['pca'].explained_variance_ratio_)

plt.rcParams["figure.figsize"] = (15,9)
fig, ax = plt.subplots()

plt.plot(xi, y, marker='o', linestyle='--', color='b')
plt.xlabel('Number of Components')
plt.xticks(np.arange(0, len(num_features), step=1))
plt.ylabel('Cumulative variance (%)')
plt.title('The number of components needed to explain variance')

plt.axhline(y=0.95, color='r', linestyle='--')
plt.text(0.5, 0.85, '95% cut-off threshold', color = 'red', fontsize=16)

ax.grid(axis='x')
plt.show()

可以看出当主成分为12个时，便可以解释原19维数据95%的方差，于是我们便可以将PCA中的n_component设为12

P.S. 后续的分析中发现在本人这一套的建模模式下，PCA没有显著好处，且会降低模型性能，于是最后没有采取PCA。

统一列转换

将前文所述的所有方法打包为一个列转换管道pipeline：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import OrdinalEncoder
from category_encoders.target_encoder import TargetEncoder
from sklearn.preprocessing import MinMaxScaler

preprocess = ColumnTransformer(transformers=[('num',
                                              Pipeline(steps=[('scaler1', RobustScaler()),
                                                              ('scaler2', StandardScaler()),
                                                             #('scaler3',MinMaxScaler()),
                                                             #('pca', PCA(n_components=12))
                                                              ]),
                                              num_features),
                                                 
                                              ('OneHotCat',
                                              Pipeline(steps=[('encoder1', OneHotEncoder(handle_unknown='ignore'))
													   ]),
                                              onehot_cat_features),
                                              ('TargetCat',
                                              Pipeline(steps=[('encoder2', TargetEncoder()),
                                                              ('scaler21', RobustScaler()),
                                                              ('scaler22', StandardScaler()),
                                                             #('scaler23', MinMaxScaler())
                                                              ]),
                                              target_cat_features),
                                              ('OrdinalCat',
                                              Pipeline(steps=[#('encoder3', OrdinalEncoder(handle_unknown='use_encoded_value', unknown_value=-1)),
                                                               ('encoder2', TargetEncoder()),
                                                               ('scaler31', RobustScaler()),
                                                               ('scaler32', StandardScaler()),
                                                              #('scaler33', MinMaxScaler())
                                                               ]),
                                              ordinal_cat_features)
                                              ])

至此，预处理管道就搭建完了。

模型选取及调参

这一部分中，我选取了6个模型：随机森林、极限梯度上升、弹力网回归、轻量梯度上升、套索回归、岭回归。

而调参环节，我采用的调参器是optuna，这是一个声称有很好的算法的调参框架。而实际使用上，相比网格搜索，它的性能也高很多，且可以看到调参进度，避免了使用GridSearch框架时看不出程序是否卡死的烦恼；同时，它还自带一些可视化方法，可以直观地看出调参过程。当然对于其具体的实现细节，本人并没有深入了解，这里只记录一下使用方法。

optuna调参的一些操作要感谢PrettyMeng 大佬的帮助。

optuna安装：

1
pip install optuna

加载模型库：

1
2
3
4
5
6
7
8
from sklearn.linear_model import Lasso,  Ridge
from sklearn.ensemble import RandomForestRegressor
import xgboost as xgb
import lightgbm as lgb
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import mean_squared_error

import optuna

极限梯度上升模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
def objective_xgb(trial, X_train, y_train_raw):
    """
    Objective function to tune an `XGBRegressor` model.
    """
    y_train = np.log1p(y_train_raw)

    # Define Parameter Grid to Tune
    params = {
        'n_estimators': trial.suggest_int("n_estimators", 100, 5000),
        'reg_alpha': trial.suggest_loguniform("reg_alpha", 1e-10, 1e-1),
        'reg_lambda': trial.suggest_loguniform("reg_lambda", 1e-8, 100.0),
        "subsample": trial.suggest_float("subsample", 0.8, 1.0, step=0.001),
        "learning_rate": trial.suggest_float("learning_rate", 0.01, 0.1, log=True),
        'max_depth': trial.suggest_int("max_depth", 2, 9),
        'colsample_bytree': trial.suggest_float('colsample_bytree', 0, 1.0, step=0.05),
        'colsample_bylevel': trial.suggest_float('colsample_bylevel', 0.5, 1.0, step=0.005),
        'colsample_bynode': trial.suggest_float('colsample_bynode', 0, 1.0, step=0.05),
        "gamma": trial.suggest_float("gamma", 0, 0.1, step=0.0005),
        "min_child_weight": trial.suggest_int("min_child_weight", 0, 10),
        'nthread': -1,
        'booster': "gbtree",
        'objective': "reg:squarederror",
        'early_stopping_rounds': 300,
        'random_state': 42,
        'eval_metric': "rmse"
    }
    
    # Tune pruning
    # from optuna.integration import XGBoostPruningCallback
    # pruning_callback = XGBoostPruningCallback(trial, "validation_0-rmse")

    
    model = xgb.XGBRegressor(
        # callbacks=[pruning_callback],
        **params
    )
    
    # Check and enable GPU accelerate
    GPU_ENABLED = True
    if GPU_ENABLED:
        params["tree_method"] = "gpu_hist"
        params["predictor"] = "gpu_predictor"

    # K-Fold CV
    kf = KFold(n_splits=5, shuffle=True, random_state=2022)
    kf.split(X_train, y_train)
    rmse = []
    for train_index, valid_index in kf.split(X_train, y_train):
        X_trainS, X_validS = X_train.iloc[train_index], X_train.iloc[valid_index]
        y_trainS, y_validS = y_train.iloc[train_index], y_train.iloc[valid_index]
        X_trainS = preprocess.fit_transform(X_trainS, y_trainS)
        X_validS = preprocess.transform(X_validS)

        model.fit(
            X_trainS,
            y_trainS,
            eval_set=[(X_validS, y_validS)],
            verbose=False
        )
        
        yhat = model.predict(X_validS)
        rmse.append(mean_squared_error(y_validS, yhat, squared=False))
    rmse = sum(rmse) / len(rmse)
    return rmse

study_xgb = optuna.create_study(study_name="XGB Tuner", direction="minimize")
study_xgb.optimize(
    lambda trial: objective_xgb(
        trial,
        X_train,
        y_train_raw),
    n_trials=300)
xgbBestPara = study_xgb.best_params
print(
    f'Best Parameter: {study_xgb.best_params}\nBest Score: {study_xgb.best_value}')
	
# Best Parameter: {'n_estimators': 3294, 'reg_alpha': 1.929897932989974e-10, 'reg_lambda': 1.0186659359903715e-07, 'subsample': 0.8460000000000001, 'learning_rate': 0.0123668789206247, 'max_depth': 3, 'colsample_bytree': 0.30000000000000004, 'colsample_bylevel': 0.6000000000000001, 'colsample_bynode': 0.75, 'gamma': 0.007, 'min_child_weight': 0}
# Best Score: 0.11385928560228975

随机森林模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
def objective_rf(trial, X_train, y_train_raw):
    """
    Objective function to tune an `RandomForestRegressor` model.
    """
    
    y_train = np.log1p(y_train_raw)

    params = {
        'n_estimators': trial.suggest_int('n_estimators', 400, 800),
        'max_features': trial.suggest_uniform('max_features', 0.1, 0.5),
        'min_samples_split': trial.suggest_int('min_samples_split', 2, 5),
        'min_samples_leaf': trial.suggest_int('min_samples_leaf', 1, 5),
        'max_samples': trial.suggest_uniform('max_samples', 0.8, 1)
    }

    model = RandomForestRegressor(n_jobs=-1,
                                  random_state=44,
                                  **params)
    
    modelP = Pipeline(steps = [("pre", preprocess),
                               ("model", model)
                               ])

    rmse = np.sqrt(-cross_val_score(modelP, X_train, y_train, 
                                    n_jobs=-1, 
                                    cv=5, 
                                    scoring="neg_mean_squared_error")).mean()
    return rmse


study_rf = optuna.create_study(direction="minimize")
study_rf.optimize(
    lambda trial: objective_rf(
        trial,
        X_train,
        y_train_raw),
    n_trials=300)

rfBestPara = study_rf.best_params
print(
    f'Best Parameter: {study_rf.best_params}\nBest Score: {study_rf.best_value}')
	
# Best Parameter: {'n_estimators': 601, 'max_features': 0.2540470909182003, 'min_samples_split': 5, 'min_samples_leaf': 1, 'max_samples': 0.9999286526034251}
# Best Score: 0.13323499907488073

轻量梯度上升模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
def objective_lgb(trial, X_train, y_train_raw):
    """
    Objective function to tune an `lgb` model.
    """
    
    y_train = np.log1p(y_train_raw)

    # Define Parameter Grid to Tune
    params = {
        'objective': 'regression',
        'metric': 'rmse',
        'verbosity': -1,
        'boosting_type': 'gbdt',
        'reg_alpha': trial.suggest_loguniform('reg_alpha', 1e-6, 1e-3),
        'reg_lambda': trial.suggest_loguniform('reg_lambda', 1e-8, 10.0),
        'num_leaves': trial.suggest_int('num_leaves', 2, 20),
        # 'learning_rate': trial.suggest_loguniform('learning_rate', 1e-8, 1.0),
        'learning_rate': 0.01,
        'n_estimators': trial.suggest_int('n_estimators', 4500, 8500),
        'colsample_bytree': trial.suggest_uniform('colsample_bytree', 0.8, 0.9),
        'subsample': trial.suggest_uniform('subsample', 0.001, 1.0),
        #'bagging_freq': trial.suggest_int('bagging_freq', 1, 7),
        'min_child_samples': trial.suggest_int('min_child_samples', 1, 5)
        }

    # Tune pruning
    # from optuna.integration import LightGBMPruningCallback
    
    # pruning_callback = LightGBMPruningCallback(trial, "rmse")


    
    model = lgb.LGBMRegressor(
        random_state=42,
        **params
    )
    
    callbacks = [lgb.early_stopping(300, verbose=0), 
                 lgb.log_evaluation(period=0), 
                #  pruning_callback
                 ]
    
    # K-Fold CV
    kf = KFold(n_splits=5, shuffle=True, random_state=2022)
    kf.split(X_train, y_train)
    rmse = []
    for train_index, valid_index in kf.split(X_train, y_train):
        X_trainS, X_validS = X_train.iloc[train_index], X_train.iloc[valid_index]
        y_trainS, y_validS = y_train.iloc[train_index], y_train.iloc[valid_index]
        X_trainS = preprocess.fit_transform(X_trainS, y_trainS)
        X_validS = preprocess.transform(X_validS)

        model.fit(
            X_trainS,
            y_trainS,
            eval_set=[(X_validS, y_validS)],
            callbacks=callbacks
        )
        
        yhat = model.predict(X_validS)
        rmse.append(mean_squared_error(y_validS, yhat, squared=False))
    rmse = sum(rmse) / len(rmse)
    return rmse

study_lgb = optuna.create_study(direction="minimize")
study_lgb.optimize(
    lambda trial: objective_lgb(
        trial,
        X_train,
        y_train_raw),
    n_trials=300)
lgbBestPara = study_lgb.best_params
print(f'Best Parameter: {study_lgb.best_params}\nBest Score: {study_lgb.best_value}')

# Best Parameter: {'reg_alpha': 2.440166117521566e-05, 'reg_lambda': 0.006869171906469875, 'num_leaves': 4, 'n_estimators': 6623, 'colsample_bytree': 0.8246153451262771, 'subsample': 0.39754188623980913, 'min_child_samples': 3}
# Best Score: 0.11849003568984647

弹力网回归模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
from sklearn.linear_model import ElasticNet


def objective_elas(trial, X_train, y_train_raw):
    """
    Objective function to tune an `ElasticNet` model.
    """
    
    y_train = np.log1p(y_train_raw)

    # Define Parameter Grid to Tune
    params = {
        'alpha': trial.suggest_loguniform('alpha', 0.001, 1),
        'l1_ratio': trial.suggest_loguniform('l1_ratio', 0.001, 0.2)
    }

    model = ElasticNet(
        random_state=44,
        max_iter=100000000,
        **params
    )

    # K-Fold CV
    kf = KFold(n_splits=5, shuffle=True, random_state=2022)
    kf.split(X_train, y_train)
    rmse = []
    for train_index, valid_index in kf.split(X_train, y_train):
        X_trainS, X_validS = X_train.iloc[train_index], X_train.iloc[valid_index]
        y_trainS, y_validS = y_train.iloc[train_index], y_train.iloc[valid_index]
        X_trainS = preprocess.fit_transform(X_trainS, y_trainS)
        X_validS = preprocess.transform(X_validS)

        model.fit(
            X_trainS,
            y_trainS
        )

        yhat = model.predict(X_validS)
        rmse.append(mean_squared_error(y_validS, yhat, squared=False))
    rmse = sum(rmse) / len(rmse)
    return rmse


study_elas = optuna.create_study(direction="minimize")
study_elas.optimize(
    lambda trial: objective_elas(
        trial,
        X_train,
        y_train_raw),
    n_trials=300
    )
elasBestPara = study_elas.best_params
print(f'Best Parameter: {study_elas.best_params}\nBest Score: {study_elas.best_value}')

# Best Parameter: {'alpha': 0.05413710739105013, 'l1_ratio': 0.019619883123773534}
# Best Score: 0.1441800147792022

套索回归模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
def objective_lasso(trial, X_train, y_train_raw):
    """
    Objective function to tune an `Lasso` model.
    """
    
    y_train = np.log1p(y_train_raw)

    model = Lasso(
        max_iter=10000000,
        alpha=trial.suggest_loguniform('alpha', 1e-4, 2e-3)
    )

    # K-Fold CV
    kf = KFold(n_splits=5, shuffle=True, random_state=2022)
    kf.split(X_train, y_train)
    rmse = []
    for train_index, valid_index in kf.split(X_train, y_train):
        X_trainS, X_validS = X_train.iloc[train_index], X_train.iloc[valid_index]
        y_trainS, y_validS = y_train.iloc[train_index], y_train.iloc[valid_index]
        X_trainS = preprocess.fit_transform(X_trainS, y_trainS)
        X_validS = preprocess.transform(X_validS)

        model.fit(
            X_trainS,
            y_trainS
        )

        yhat = model.predict(X_validS)
        rmse.append(mean_squared_error(y_validS, yhat, squared=False))
    rmse = sum(rmse) / len(rmse)
    return rmse


study_lasso = optuna.create_study(direction="minimize")
study_lasso.optimize(
    lambda trial: objective_lasso(
        trial,
        X_train,
        y_train_raw),
    n_trials=300
    )
lassoBestPara = study_lasso.best_params
print(f'Best Parameter: {study_lasso.best_params}\nBest Score: {study_lasso.best_value}')

# Best Parameter: {'alpha': 0.001211363074795742}
# Best Score: 0.14435096531753505

岭回归模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
def objective_ridge(trial, X_train, y_train_raw):
    """
    Objective function to tune an `Ridge` model.
    """
    
    y_train = np.log1p(y_train_raw)
    
    # Define Parameter Grid to Tune
    params = {
        'alpha': trial.suggest_loguniform('alpha', 94, 98)
    }

    model = Ridge(
        **params
    )

    # K-Fold CV
    kf = KFold(n_splits=5, shuffle=True, random_state=2022)
    kf.split(X_train, y_train)
    rmse = []
    for train_index, valid_index in kf.split(X_train, y_train):
        X_trainS, X_validS = X_train.iloc[train_index], X_train.iloc[valid_index]
        y_trainS, y_validS = y_train.iloc[train_index], y_train.iloc[valid_index]
        X_trainS = preprocess.fit_transform(X_trainS, y_trainS)
        X_validS = preprocess.transform(X_validS)

        model.fit(
            X_trainS,
            y_trainS
        )

        yhat = model.predict(X_validS)
        rmse.append(mean_squared_error(y_validS, yhat, squared=False))
    rmse = sum(rmse) / len(rmse)
    return rmse


study_ridge = optuna.create_study(direction="minimize")
study_ridge.optimize(
    lambda trial: objective_ridge(
        trial,
        X_train,
        y_train_raw),
    n_trials=300
    )
ridgeBestPara = study_ridge.best_params
print(f'Best Parameter: {study_ridge.best_params}\nBest Score: {study_ridge.best_value}')

# Best Parameter: {'alpha': 96.39298499008997}
# Best Score: 0.14449888940471906

模型堆叠与混合

模型堆叠(Stacking)

在上述的模型中，极限梯度上升XGB的实测性能最好，然而，为了让其它的模型也能用到，这里我们考虑将所有上述模型进行堆叠，将他们用为一层基线模型，然后用岭回归作为二层元模型。我们使用StackingRegressor来实现。

首先将所有调到的最优参数储存，并搭建每一个模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
xgbBestPara = {'n_estimators': 3294, 
               'reg_alpha': 1.929897932989974e-10,
               'reg_lambda': 1.0186659359903715e-07, 
               'subsample': 0.8460000000000001,
               'learning_rate': 0.0123668789206247,
               'max_depth': 3, 
               'colsample_bytree': 0.30000000000000004, 
               'colsample_bylevel': 0.6000000000000001,
               'colsample_bynode': 0.75,
               'gamma': 0.007, 
               'min_child_weight': 0}

lgbBestPara = {'reg_alpha': 2.440166117521566e-05,
               'reg_lambda': 0.006869171906469875,
               'num_leaves': 4,
               'n_estimators': 6623,
               'colsample_bytree': 0.8246153451262771,
               'subsample': 0.39754188623980913,
               'min_child_samples': 3}

elasBestPara = {'alpha': 0.05413710739105013, 
                'l1_ratio': 0.019619883123773534}

rfBestPara = {'n_estimators': 601,
              'max_features': 0.2540470909182003,
              'min_samples_split': 5,
              'min_samples_leaf': 1,
              'max_samples': 0.9999286526034251}

ridgeBestPara = {'alpha': 96.39298499008997}

lassoBestPara = {'alpha': 0.001211363074795742}

modelXGB = Pipeline(steps=[("pre", preprocess),
                           ("model", xgb.XGBRegressor(
                               booster="gbtree",
                               objective="reg:squarederror",
                               random_state=42,
                               **xgbBestPara
                           ))
                           ])

modelLGB = Pipeline(steps=[("pre", preprocess),
                           ("model", lgb.LGBMRegressor(
                               random_state=42,
                               **lgbBestPara
                           ))
                           ])

modelElastic = Pipeline(steps=[("pre", preprocess),
                               ("model", ElasticNet(
                                   random_state=44,
                                   max_iter=100000000,
                                   **elasBestPara
                               ))
                               ])

modelRf = Pipeline(steps=[("pre", preprocess),
                          ("model", RandomForestRegressor(
                              n_jobs=-1,
                              random_state=44,
                              **rfBestPara
                          ))
                          ])


modelRidge = Pipeline(steps=[("pre", preprocess),
                             ("model", Ridge(
                              **ridgeBestPara
                              ))
                             ])

modelLasso = Pipeline(steps=[("pre", preprocess),
                             ("model", Lasso(
                                 max_iter=10000000,
                                 **lassoBestPara))
                             ])

然后进行堆叠：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.ensemble import StackingRegressor

estimators = [('xgb', modelXGB),
              ('lgb', modelLGB),
              ('elastic', modelElastic),
              ('rf', modelRf),
              ('lasso', modelLasso),
              ('ridge', modelRidge)
              ]
reg = StackingRegressor(estimators=estimators,
                        n_jobs=-1,
                        verbose=2,
                        cv=5,
                        final_estimator=Ridge(max_iter=10000000)
                        )
y_train = np.log1p(y_train_raw)

reg.fit(X_train, y_train)
y_pred = np.expm1(reg.predict(X_test))

堆叠出来的模型实测有所提升，大概提升了40名左右。

模型混合(Blending)

做完堆叠后，我们可以考虑将堆叠模型和其他所有模型进行混合，即每个模型分别做预测，然后按一定权重进行混合，得到最终结果。某种意义上，这个和上述的堆叠的二层元模型做的事情很像（如果元模型选的是线性回归的话），但实测下来是有提升的，于是本人也就懒得去探讨其具体的区别了，先用上再说。当然这里的权重是本人随便设置的，不是很严谨，最好的是根据测试集进行调整，但由于时间原因，就不在这个项目里做了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def BlendingModel(X_train, y_train, X_test):
    xgbPredict = modelXGB.fit(X_train, y_train).predict(X_test)
    lgbPredict = modelLGB.fit(X_train, y_train).predict(X_test)
    elasticPred = modelElastic.fit(X_train, y_train).predict(X_test)
    rfPred = modelRf.fit(X_train, y_train).predict(X_test)
    lassoPred = modelLasso.fit(X_train, y_train).predict(X_test)
    ridgePred = modelRidge.fit(X_train, y_train).predict(X_test)

    stackPred = reg.fit(X_train, y_train).predict(X_test)
    blended_pred = (0.05*xgbPredict +
                    0.1*lgbPredict +
                    0.05*elasticPred +
                    0*rfPred +
                    0.05*lassoPred +
                    0.04*ridgePred +
                    0.71*stackPred
                    )

    return blended_pred


blend_pred = np.expm1(BlendingModel(X_train, y_train, X_test))

这一步做完大概提升了100多名的样子。

结果输出

最终提交给Kaggle的数据需要根据其要求进行格式化，这一步就是很基础的表操作，不细说了。

1
2
3
4
BLENDcsv = test_raw.copy()
BLENDcsv['SalePrice'] = blend_pred
BLENDcsv['Id'] = test_ID
BLENDcsv[['Id', 'SalePrice']].set_index('Id').to_csv('BLEND.csv')

将csv提交后便可以得到成绩啦！

这个排名和大佬总归是不能比的，但作为一个刚入门的新手，本人觉得能拿到Top15%就已经可以接受了。当然其实这个名次是可以优化的，主要就是上述的模型混合部分，具体权重我认为是还有些操作空间的，这就留给未来再说吧，目前这个成绩就足以应付课程期末了。