机器学习基础笔记（二）

发表于 更新于 分类于 阅读次数： 本文字数： 12k 阅读时长 ≈ 11 分钟

banner

前言

在上一篇文章[机器学习基础笔记（一）]中，笔者整理了机器学习这门课上半节的课程内容，由于博客目录存在容量上限，之后的内容目录会无法显示，因此为了美观起见，在此重开一篇文章，作为该系列的第二部分

当然，目前课程还未结束，本文会随着课程进度，同步更新。

由于当前内容已经超出本文目录结构所能承载的极限，故本文完结，后续内容将在[机器学习基础笔记（三）]中继续。

树，森林，与集成学习(Trees, Forests & Ensembles)

这个标题看着竟然有些文艺。

树模型(Tree Models)

简介是网上复制来的：

决策树(Decision Tree)是树模型中最简单的一个模型，也是后面将要介绍到的随机深林与梯度提升决策树两个模型的基础。利用决策树算法，在历史数据集上，我们可以画出这样一个树，这颗树上的叶子节点表示结论，非叶子节点表示依据。一个样本根据自身特征，从根节点开始，根据不同依据决策，拆分成子节点，直到只包含一种类别(即一种结论)的叶子节点为止。

代码：

1
2
3
4
from sklearn.tree import DecisionTreeRegressor

tree = DecisionTreeRegressor()
tree.fit(X_train, y_train)

可以用这个代码可视化：

1
2
3
4
5
from sklearn.tree import plot_tree
%matplotlib inline
fig = plt.figure(figsize=(25,20))
_ = plot_tree(tree, 
                   filled=True)

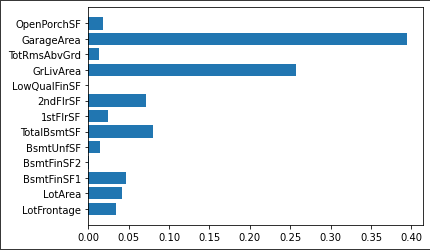
特征重要性：

1
plt.barh(cols, tree.feature_importances_)

当然，单一树模型不调参会有过拟合问题，因此进行网格搜索调参：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
regtree = DecisionTreeRegressor()

parameters={"splitter":["best","random"],
            "max_depth" : [1,3,5],
           "min_samples_leaf":[1,2,3,4,5],
           "min_weight_fraction_leaf":[0.1,0.2,0.3],
           "max_features":["auto","log2","sqrt",None],
           "max_leaf_nodes":[None,10,20] }
		   
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error, make_scorer

my_mse = make_scorer(mean_squared_error, greater_is_better=False)

tuning_model = GridSearchCV(regtree, 
                            param_grid=parameters,
                            scoring=my_mse,
                            cv=3,)

tuning_model.fit(X_train, y_train)

tuning_model.best_params_

得到：

1
2
3
4
5
6
{'max_depth': 5,
 'max_features': 'log2',
 'max_leaf_nodes': 20,
 'min_samples_leaf': 4,
 'min_weight_fraction_leaf': 0.1,
 'splitter': 'best'}

集成学习(Ensemble Learning)

定义是网上复制来的：

集成学习(Ensemble Learning)算法的基本思想就是将多个分类器组合，从而实现一个预测效果更好的集成分类器。

随机森林模型(Random Forests)

定义是网上复制来的：

随机森林，顾名思义，是用随机的方式建立一个森林，森林里面有很多的树模型，随机森林的每一棵树之间是没有关联的。 在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。

代码：

1
2
3
4
from sklearn.ensemble import RandomForestRegressor

for1 = RandomForestRegressor()
for1_fit = for1.fit(X_train, y_train)

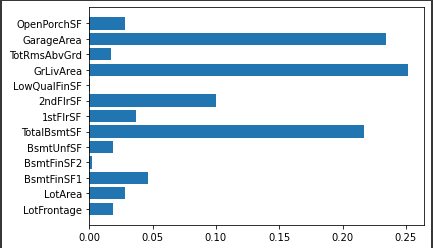
特征重要性：

1
plt.barh(cols, for1.feature_importances_)

调参：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
rantree = RandomForestRegressor()

parameters={'bootstrap': [True],
            'max_depth': [80, 90, 100],
            'max_features': ['auto', 'sqrt'],
            'min_samples_leaf': [2, 3],
            'min_samples_split': [3, 4, 5],
            'n_estimators': [200, 400]}

from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error, make_scorer

my_mse = make_scorer(mean_squared_error, greater_is_better=False)

tuning_model = GridSearchCV(rantree, 
                            param_grid=parameters,
                            scoring=my_mse,
                            cv=3,
                            n_jobs = -1, 
                            verbose = 2)
							
tuning_model.fit(X_train, y_train)

tuning_model.best_params_

得到：

1
2
3
4
5
6
{'bootstrap': True,
 'max_depth': 80,
 'max_features': 'sqrt',
 'min_samples_leaf': 2,
 'min_samples_split': 3,
 'n_estimators': 200}

梯度上升模型(Gradient Boosting Trees)

不介绍定义以及数学原理了，需要的时候搜索一下就行，主要记录下一些代码实现。

1
2
3
4
from sklearn.ensemble import GradientBoostingRegressor

for2 = GradientBoostingRegressor()
for2_fit = for2.fit(X_train, y_train)

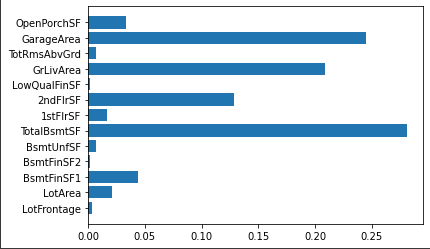
特征重要性：

1
plt.barh(cols, for2.feature_importances_)

调参：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
gratree = GradientBoostingRegressor()

parameters={'max_depth': [80, 90, 100],
            'max_features': ['auto', 'sqrt'],
            'min_samples_leaf': [2, 3],
            'min_samples_split': [3, 4, 5],
            'n_estimators': [200, 400]}

from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error, make_scorer

my_mse = make_scorer(mean_squared_error, greater_is_better=False)

tuning_model2 = GridSearchCV(gratree, 
                            param_grid=parameters,
                            scoring=my_mse,
                            cv=3,
                            n_jobs = -1, 
                            verbose = 2)

tuning_model2_fit = tuning_model2.fit(X_train, y_train)
tuning_model2_fit.best_params_

究极梯度上升(XGBoost)

其实这个中文翻译大家都是叫极限梯度上升的，但本人图一乐，觉得“究极”这词看起来有趣一些，就在本文里这么叫了，大佬轻喷。

这部分不仔细写了，和上述三个是大同小异的。

线性分类模型(Linear Models for Classification)

逻辑回归(Logistic Regression)

逻辑回归，是用来做分类的一种线性模型。由于本学渣的数学知识储备不足以理解明白这模型的底层实现原理，这里就不多写了。

1
2
3
4
5
6
7
8
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import RobustScaler

steps = [('Rescale', RobustScaler()),
         ('lr', LogisticRegression())]
		 
model = Pipeline(steps)

支持向量机(Support Vactor Machine)

支持向量机，简称SVM，是一种分类器算法。

具体数学原理超出本人能力，就不在这里描述了。

边界(Margin)

当数据集可以严格二分时，设置硬边界(Hard Margin)，否则设置软边界(Soft Margin)。

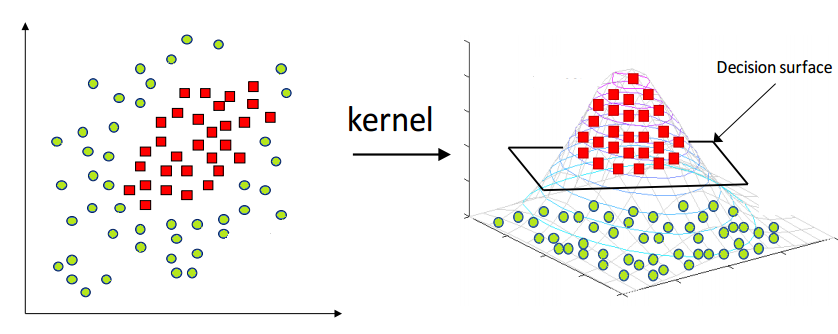
核函数(Kernel )

当数据不可线性分割时，通过设置核函数(Kernel Fuction)升维，然后在高维数据中获取超平面(HyperPlane)，再将超平面降维得到边界函数。

用于升维的核函数有很多，如RBF核、多项式核、Sigmoid核等等。一般RBF可以作为一切数据的核函数，当然容易会有过拟合问题。

要调的参数为C和gamma，调节前需要对数据放缩。

网格搜索调参：

1
2
3
4
5
param_grid = {'svc__C': np.logspace(-3, 2, 6),
			  'svc__gamma': np.logspace(-3, 2, 6) / X_train.shape[1]}

grid = GridSearchCV(scaled_svc, param_grid=param_grid, cv=10)
grid.fit(X_train, y_train)

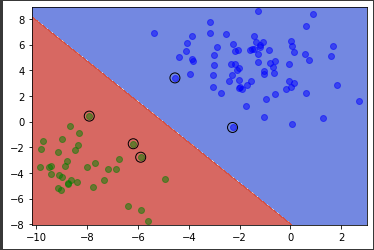
搭建一个简单的Pipeline并对支持向量可视化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.pipeline import Pipeline

scaler = StandardScaler()
model = Pipeline([('scaler', scaler), ('svc', SVC(kernel='linear'))])

model.fit(X.values, y)

### sample code for plotting decision boundaries ###

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# create a grid
x_min, x_max = df.iloc[:, 0].min() - 0.3, df.iloc[:, 0].max() + 0.3
y_min, y_max = df.iloc[:, 1].min() - 0.3, df.iloc[:, 1].max() + 0.3
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))

# get model predictions for all points on the grid
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])

# plot decision regions and boundaries
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)

# plot original data points
plt.scatter(df[df.label == 0].x, df[df.label == 0].y, marker = 'o', color = 'blue', 
            alpha = 0.5, label = 'label = 0')
plt.scatter(df[df.label == 1].x, df[df.label == 1].y, marker = 'o', color = 'green', 
            alpha = 0.5, label = 'label = 1')

########### add your code here to plot support vectors ##############
support_vectors = scaler.inverse_transform(model[1].support_vectors_)
plt.scatter(
    support_vectors[:, 0],
    support_vectors[:, 1],
    s=100,
    linewidth=1,
    facecolors="none",
    edgecolors="k",
)

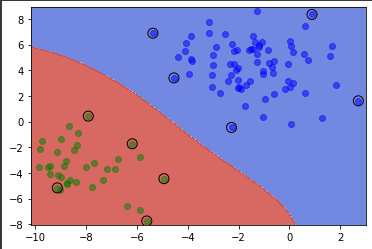
为支持向量机加核函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
model = Pipeline([('scaler', scaler), ('svc', SVC(gamma='auto', kernel='rbf', C=1, class_weight='balanced'))])
model.fit(X.values, y)


### sample code for plotting decision boundaries ###

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# create a grid
x_min, x_max = df.iloc[:, 0].min() - 0.3, df.iloc[:, 0].max() + 0.3
y_min, y_max = df.iloc[:, 1].min() - 0.3, df.iloc[:, 1].max() + 0.3
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))

# get model predictions for all points on the grid
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])

# plot decision regions and boundaries
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)

# plot original data points
plt.scatter(df[df.label == 0].x, df[df.label == 0].y, marker = 'o', color = 'blue', 
            alpha = 0.5, label = 'label = 0')
plt.scatter(df[df.label == 1].x, df[df.label == 1].y, marker = 'o', color = 'green', 
            alpha = 0.5, label = 'label = 1')

########### add your code here to plot support vectors ##############
support_vectors = scaler.inverse_transform(model[1].support_vectors_)
plt.scatter(
    support_vectors[:, 0],
    support_vectors[:, 1],
    s=100,
    linewidth=1,
    facecolors="none",
    edgecolors="k",
)

模型评估(Model evaluation)

当我们基于各种算法，得到了一个分类器后，我们自然地就想知道，手头的这个分类器的性能如何。然而，什么是“性能好”，什么是“性能坏”呢？这里的量度该如何确定呢？

可能直觉上，我们会将测试数据输入模型，得到预测结果，用预测结果与实际数据对比，如果预测的正确率越高，同时错误率越低，则我们认为模型越好。

然而，用这样的量度训练模型，则会出现一些问题，如：

  • 例1：恐怖分子识别任务。这是一个二分问题，恐怖分子计为正，非恐怖分子记为负。

    这个任务的特点是：正例负例分布非常不平均，因为恐怖分子的数量远远小于非恐怖分子的数量。假设一个数据集内的恐怖分子与非恐怖分子数量比例为1:999999999，此时我们引入一个二分类判别模型，它的行为是将所有样例都识别为负例（非恐怖分子），那么在这个数据集上该模型的准确率高达99.9999999%（因为大部分都不是恐怖分子），但恐怕没有任何一家航空公司会为这个模型买单，因为它永远不会识别出恐怖分子，航空公司更关注有多少恐怖分子被识别了出来。

现实中这样的例子还有很多，在一背景下，我们需要一些新量度，来多方位的评判模型。

混淆矩阵(Confusion Matrix)

混淆矩阵是将一些模型评估量度可视化的一种方法，其记录真阳性(True Positive)、假阳性(False Positive)、真阴性(True Negative)、假阴性(True Negative)四个数据，这几个量度内容如下图，很生动了，本人就不再赘述。

将混淆矩阵中的量度进行一些计算，则可以得到新的指标：

精确率(Precision):

$Precision = \frac{TP}{TP+FP}$

Precision描述了正例结果中有多少是真实正例，即该二分类器预测的正例有多少是准确的

召回率(Recall)

$Recall = \frac{TP}{TP+FN}$

Recall描述了模型找到正例的能力

F值(F-Score)

$F = \frac{2Precision*Recall}{Precision + Recall}$

通过更改阈值(Threshold)可以得到不同的结果：

1
2
3
4
5
6
data = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
 data.data, data.target, stratify=data.target, random_state=0)
lr = LogisticRegression().fit(X_train, y_train)
y_pred = lr.predict(X_test)
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.91 0.92 0.92 53
1 0.96 0.94 0.95 90
avg/total 0.94 0.94 0.94 143 
1
2
y_pred = lr.predict_proba(X_test)[:, 1] > .85
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 0.84 1.00 0.91 53
1 1.00 0.89 0.94 90
avg/total 0.94 0.93 0.93 143

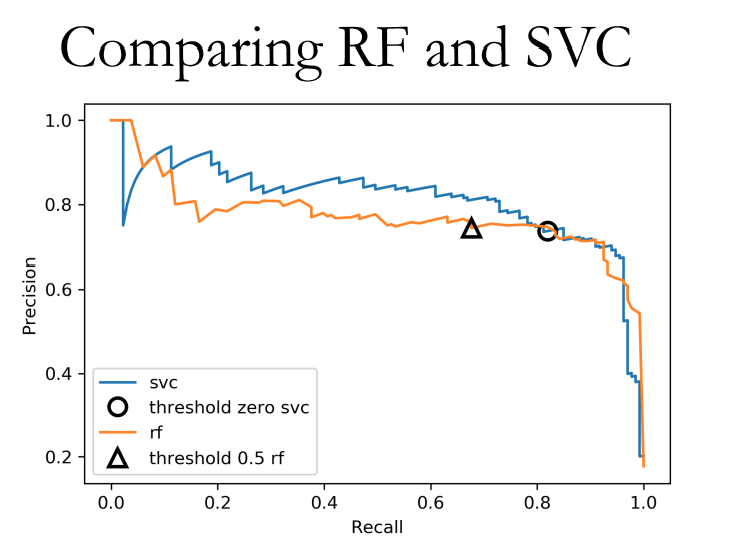
精度召回曲线(Precision-Recall Curve)

可以看到，当阈值变化时，上述指标都会变化，且Precision和Recall呈负相关，那么这两个指标的综合性能该如何体现？这时我们可以绘制Precision-Recall曲线(简称PRC)图：

1
2
3
4
5
6
X, y = make_blobs(n_samples=(2500, 500), cluster_std=[7.0, 2],
 random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y)
svc = SVC(gamma=.05).fit(X_train, y_train)
precision, recall, thresholds = precision_recall_curve(
 y_test, svc.decision_function(X_test))

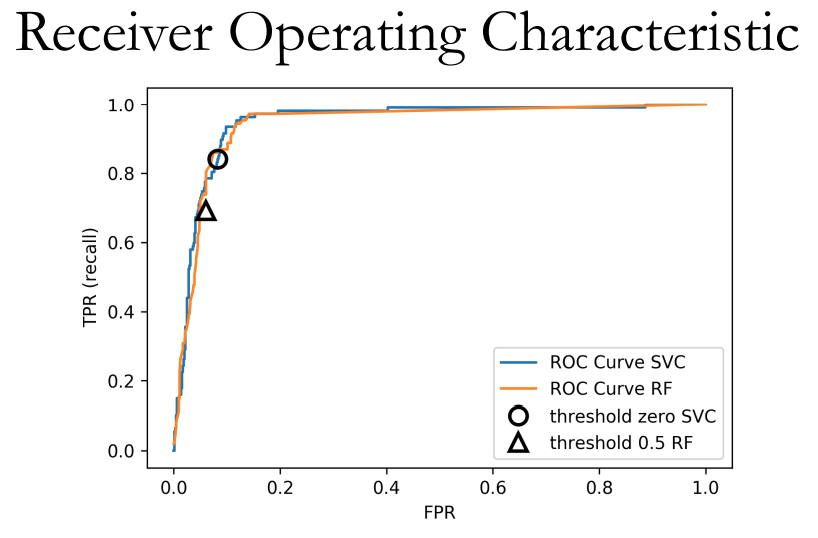
受试者工作特征曲线(Receiver Operating Characteristic Curve)

简称ROC。

与PRC相似，ROC曲线是一种评定模型对正类预测效果的曲线图。其x轴是假阳率(False Positive Rate, FPR)，y轴是真阳率(True Positive Rate, TPR)

一般我们用AUC，即曲线下方面积(Area Under Curve)作为评估。

1
2
3
4
5
from sklearn.metrics import roc_auc_score
rf_auc = roc_auc_score(y_test, rf.predict_proba(X_test)[:,1])
svc_auc = roc_auc_score(y_test, svc.decision_function(X_test))
print("AUC for random forest: {:, .3f}".format(rf_auc))
print("AUC for SVC: {:, .3f}".format(svc_auc))

AUC for random forest: 0.937
AUC for SVC: 0.916

非均衡数据(Imbalanced Data)

聚类模型(Clustering Models)

从这一章开始，我们正式进入了非监督学习的内容，而首先我们从聚类模型学起。

其实简单看来，聚类和分类很像，不同点在于我们是否预先知道数据会分为几类。

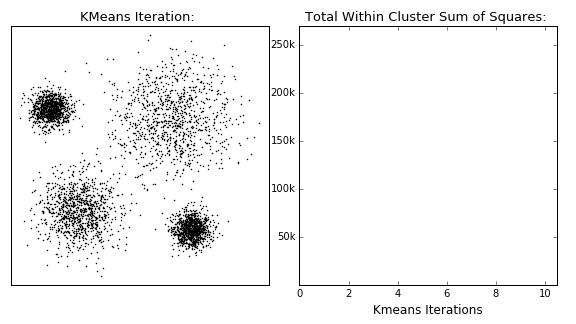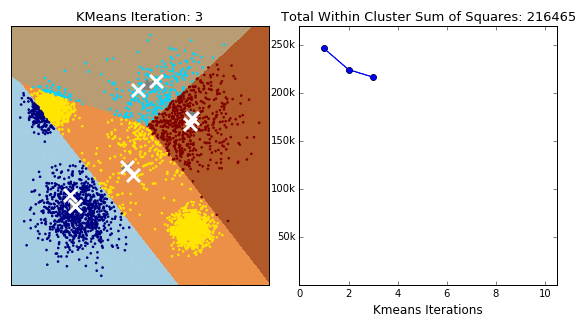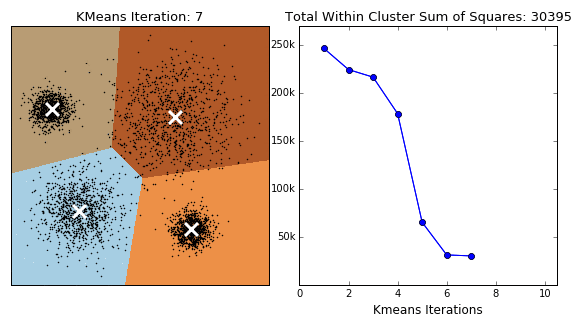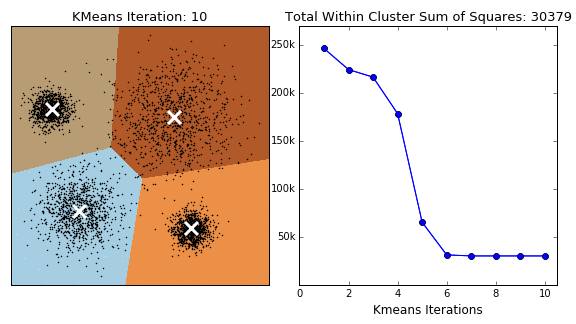
K均值算法(K-Means)

K均值算法的思路很有趣，但一两句话也讲不明白，总之是一个很动态的算法。

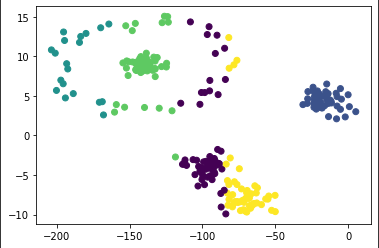
1
2
3
4
5
6
7
8
9
X, y = make_blobs(centers=4, random_state=1)
km = KMeans(n_clusters=5, random_state=0)
km.fit(X)
print(km.cluster_centers_.shape)
print(km.labels_.shape)
# predict is the same as labels_ on training data
# but can be applied to new data
print(km.predict(X).shape)
plt.scatter(X[:, 0], X[:, 1], c=km.labels_)

该算法的特点是每一个类的边界都在类中点的垂直平分线上(Clusters are Voronoi-diagrams of centers
)

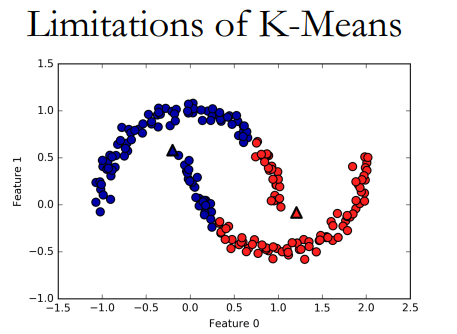
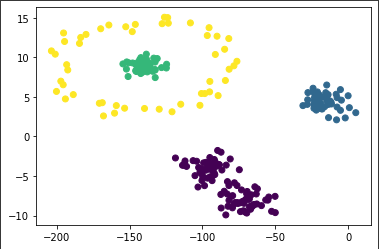
K均值的局限性在于对于这类的数据拟合力较弱：

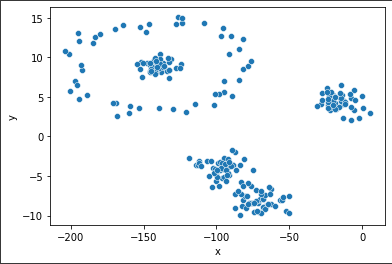
对于这样的数据集进行Kmeans：

1
2
3
4
5
6
7
import pandas as pd
df = pd.read_csv("cluster_data.csv")
X = df[['x']]
y = df.y

import seaborn as sns
sns.scatterplot(x="x", y="y", data=df)
1
2
3
4
5
6
from sklearn.cluster import KMeans
model = KMeans(n_clusters=5, random_state=0)
model.fit(X, y)

import matplotlib.pyplot as plt
plt.scatter(x = X, y = y, c=model.labels_)

可以看出其局限性。

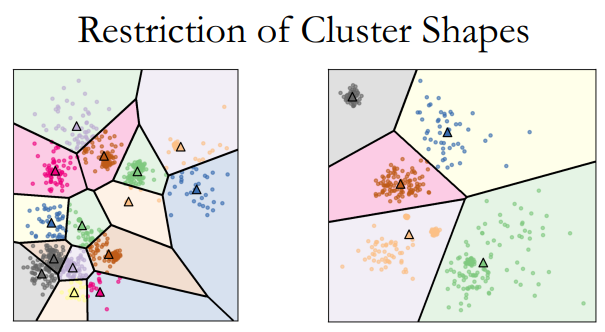
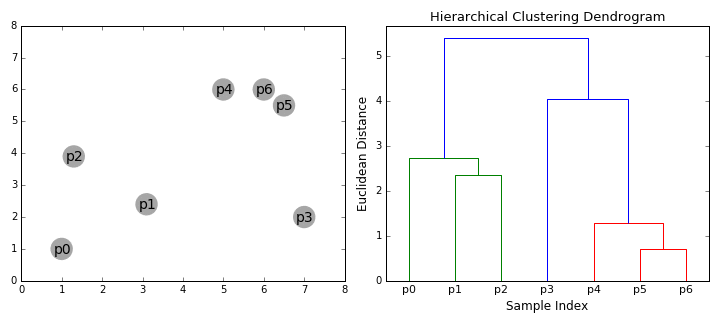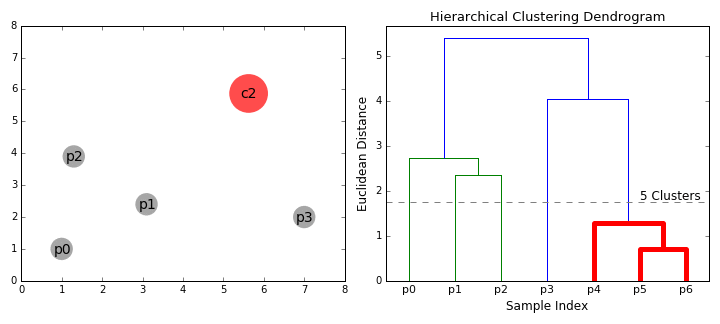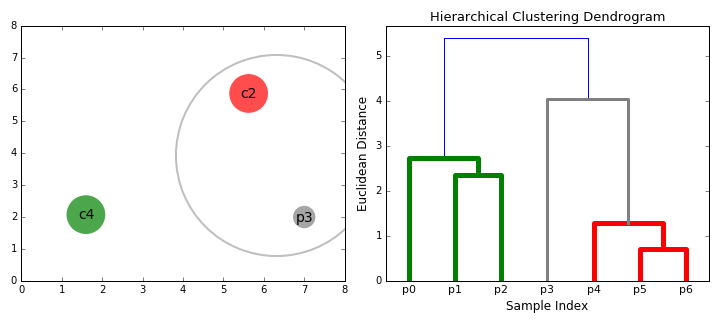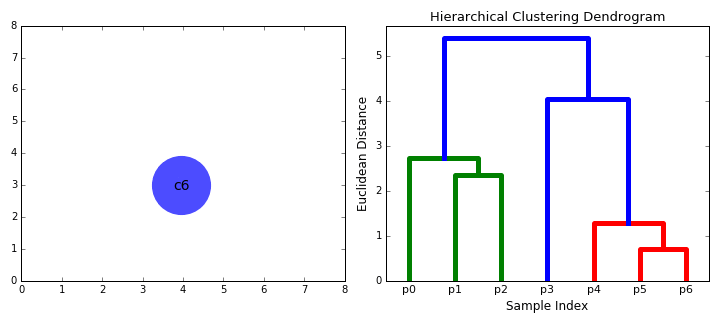
聚合聚类(Agglomerative Clustering)

聚合聚类，或者叫层次聚类(Hierarchical Clustering)，与K均值不同，此方法无需预先指定想得到的分类数量。用户在结果中选取即可：

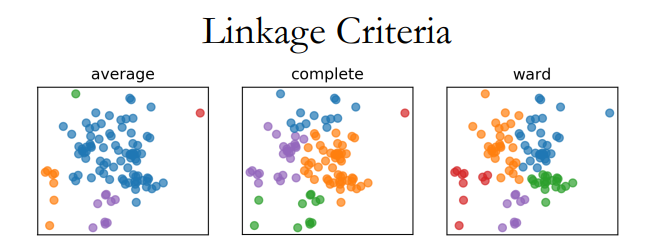
对于这种方法，需要选取不同的连接标准(Merging(Linkage) Criteria)

可以看出这类算法的局限性：连接标准的选取对于模型影响极大。

用法：

1
2
3
4
5
6
from sklearn.cluster import AgglomerativeClustering
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
model = Pipeline([('scaler', scaler), ('Agglo', AgglomerativeClustering())])
model.fit(df)

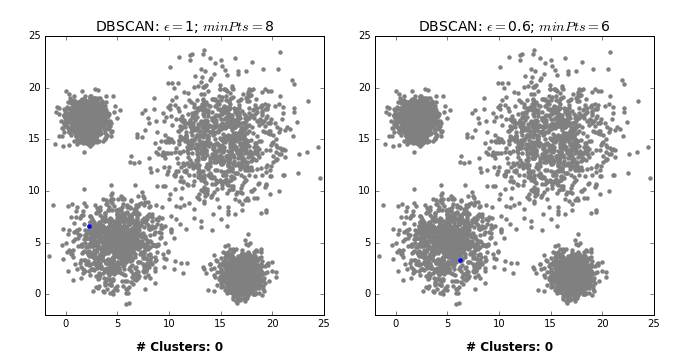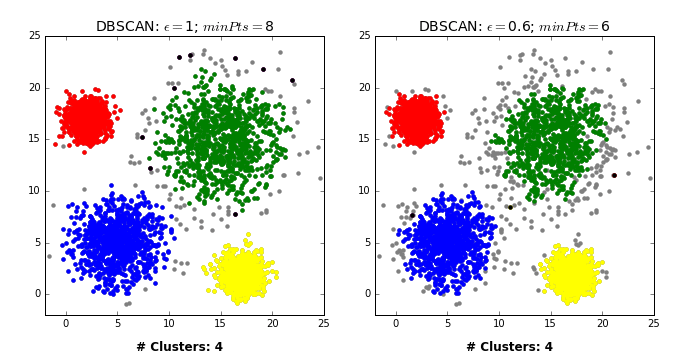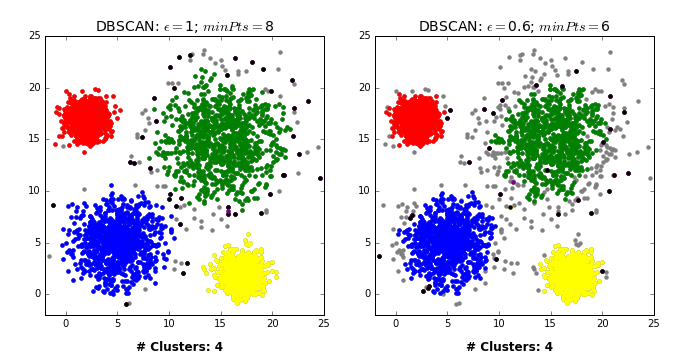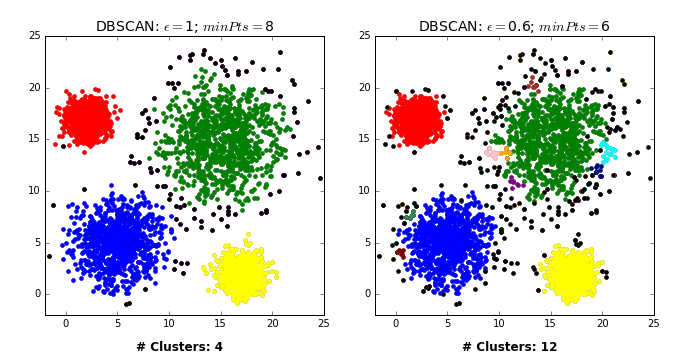
基于密度的噪点空间聚类(Density-Based Spatial Clustering of Applications with Noise)

Density-Based Spatial Clustering of Applications with Noise，简称DBSCAN。其核心思想是将密度高的点划分到统一簇中。

需要调节的参数有：

$(\epsilon,MinPt)$

对于前文提到的数据集，采取DBSCAN：

1
2
3
4
5
6
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
model = Pipeline([('scaler', scaler), ('DBSCAN', DBSCAN(eps=0.1, min_samples=4))])
model.fit(df)

plt.scatter(x = X, y = y, c=model[1].labels_)

可见在参数调整好后，效果还是可以的。

聚类特征提取(Feature Extraction)

有些时候，我们可以用聚类算法提取特征数据。

1
2
3
4
5
6
7
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
km = KMeans(n_init=1, init="random")
pipe = make_pipeline(km, LogisticRegression())
param_grid = {'kmeans__n_clusters': [10, 50, 100, 200, 500]}
grid = GridSearchCV(pipe, param_grid, cv=5, verbose=True)
grid.fit(X, y_people)

聚类模型评估(Clustering Evaluation)

轮廓系数(Silhouette Score)

一个反应聚类结果一致性的标准，可以用于评估聚类后簇与簇之间的离散程度。取值为负一到一，越大越好。

调整兰德指数(Adjusted Rand Index)

简称ARI，也是一个评价指标。数学计算这里略过，本人不搞理论研究，没什么参考必要。

目测法

字面意思，看起来是好的就是好的。

未完待续…

由于当前内容已经超出本文目录结构所能承载的极限，故本文完结，后续内容将在[机器学习基础笔记（三）]中继续。