机器学习基础笔记（三）

发表于 更新于 分类于 阅读次数： 本文字数： 17k 阅读时长 ≈ 15 分钟

banner

前言

在前两篇文章[机器学习基础笔记（一）]和[机器学习基础笔记（二）]中，笔者整理了机器学习这门课上半节的课程内容，由于博客目录存在容量上限，之后的内容目录会无法显示，因此为了美观起见，在此重开一篇文章，作为该系列的第三部分。

当然，目前课程还未结束，本文会随着课程进度，同步更新。

自然语言处理(Natural Language Processing)

截至目前，我们学习的分析方法主要建立在连续或分类特征之上，并未涉及太多图像、语言处理部分。而这一章节，我们会探讨一些简单的自然语言处理相关的技术。不过本节课涉及到的仅仅只有英文文本的处理，对于中文，则可能需进一步对以下方法进行一定程度的改进，这里就不做深入探讨了。

分词(Tokenization)

这一步无需多谈，第一步总归是将句子打散成一个一个的单词，这一过程我们叫做分词。具体如何实现我们也并不关心，交给研究算法、理论的人处理就可以了。我们只需要知道这一概念即可。

词袋(Bag of Words)

词袋法做的是：首先将每一句话进行分词，拆解为单个单词，然后将所有句子中的每一个单词都按字母表顺序放入一个“词袋”中，进而每一句话便可以表示为一个词袋的布尔行形式，最终整个文本便可以表示为一个稀疏矩阵。

代码示例：

1
2
3
4
5
6
7
8
9
malory = ["Do you want ants?", 
		  "Because that’s how you get ants."]
		  
from sklearn.feature_extraction.text import CountVectorizer
vect = CountVectorizer()
vect.fit(malory)
print(vect.get_feature_names())

# 得到词袋为： ['ants', 'because', 'do', 'get', 'how', 'that', 'want', 'you']
1
2
3
4
5
6
7
X = vect.transform(malory)
print(X.toarray())


# 得到的处理完成的文本为：
# array([[1, 0, 1, 0, 0, 0, 1, 1],
#       [1, 1, 0, 1, 1, 1, 0, 1]])

也可以查看每一句话的词袋：

1
2
3
4
5
6
7
8
9
print(malory)
print(vect.inverse_transform(X)[0])
print(vect.inverse_transform(X)[1])

# 得到：

# ['Do you want ants?', 'Because that’s how you get ants.']
# ['ants' 'do' 'want' 'you']
# ['ants' 'because' 'get' 'how' 'that' 'you']

做好词袋后，其实就已经可以进行模型拟合了，如IMDB好评/差评的预测示例：

首先我们加载数据：

1
2
3
4
5
from sklearn.datasets import load_files
reviews_train = load_files("../data/aclImdb/train/")

text_trainval, y_trainval = reviews_train.data, reviews_train.target
print("text_train[1]:\n{}".format(text_trainval[1].decode()))

其中评论内容格式如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
text_train[1]:
'Words can't describe how bad this movie is. I can't explain it by
writing only. You have too see it for yourself to get at grip of how
horrible a movie really can be. Not that I recommend you to do that.
There are so many clichés, mistakes (and all other negative things
you can imagine) here that will just make you cry. To start with the
technical first, there are a LOT of mistakes regarding the airplane. I 
won't list them here, but just mention the coloring of the plane. They
didn't even manage to show an airliner in the colors of a fictional
airline, but instead used a 747 painted in the original Boeing livery.
Very bad. The plot is stupid and has been done many times before, only
much, much better. There are so many ridiculous moments here that i
lost count of it really early. Also, I was on the bad guys' side all
the time in the movie, because the good guys were so stupid. "Executive
Decision" should without a doubt be you're choice over this one, even the
"Turbulence"-movies are better. In fact, every other movie in the world is
better than this one.'

将文本去除特殊符号并矢量化，然后进行训练、验证、测试集的分割：

1
2
3
4
5
6
7
8
9
text_train_val = [doc.replace(b"<br />", b" ") for doc in text_train_val
text_train, text_val, y_train_, y_val = train_test_split(text_trainval,
														 y_trainval,
														 stratify=y_trainval, 
														 random_state=0)
vect = CountVectorizer()
X_train = vect.fit_transform(text_train)
X_val = vect.transform(text_val)
X_train

可以看到X_train是一个稀疏矩阵：

1
2
<18750x66651 sparse matrix of type '<class 'numpy.int64'>'
 with 2580448 stored elements in Compressed Sparse Row format>

这里我们用逻辑回归模型来拟合：

1
2
from sklearn.linear_model import LogisticRegressionCV
lr = LogisticRegressionCV().fit(X_train, y_train)

得到的特征重要性如下：

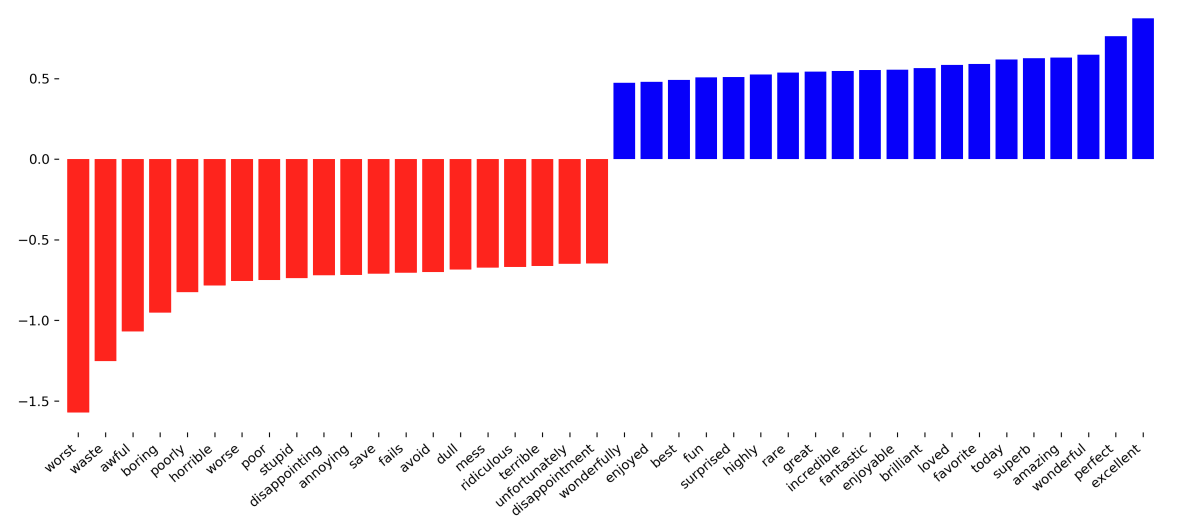
可以看出，结果还是比较符合预期的：其中积极的词汇对于好评的贡献率大，而消极的词汇对于差评的贡献率大。

文本标准化(Normalization)

我们知道，英文中同一个单词往往有不同时态、单复数等变化，而显然这些变化的词义不会改变太多，于是我们希望将这些词合并，以减少特征维度以及无意义的计算。主要方式有下述两种：

词干提取(Stemming)

英语中有单词加前后缀变形的习惯，于是，我们可以基于变形规则，直接将词缀去掉。

1
2
3
4
5
6
from nltk.stem import LancasterStemmer
lancaster=LancasterStemmer()
lancaster.stem('prestudy')
# 输出：prestudi
# study:study 
# studies:studi

当然，可以看出词干提取有一定问题：

  1. 还原出来的词干，未必是一个单词。

  2. 有的单词是一样的，但是规则却不能将他们还原成一样。

  3. 有的单词是不一样的，但是规则会把这两个单词还原成一个。

词形还原(Lemmatization)

1
2
3
4
from nltk.stem import WordNetLemmatizer
wordnet_lemmatizer = WordNetLemmatizer()
wordnet_lemmatizer.lemmatize('studies')
# 输出是study

词形还原的准确度更高，因为本质上是基于字典的查询，然而问题在于：对于字典中没有的单词，是无法进行还原的。

停用词(Stop Words)

我们知道，有很多词语并没有实质的意义，比如连词、冠词等，也就是说它们对于语义的贡献很少，故而我们考虑忽略这些词语。

这一操作的实现手段很原始：建立一个停用词库，如果词汇出现在词库中则被忽略。当然，停用词库是需要手动建立的，目前已经有许多过去的从业者建立的停用词库可供选择。

除了主观判断，具体的建立停用词库的标准也是有的，但涉及到的知识比较复杂，超出本人理论知识范畴了，鉴于本人也不是PhD，这里我们就不对理论做过多研究了。

1
2
3
4
5
vect = CountVectorizer(stop_words='english')
vect.fit(malory)
print(vect.get_feature_names())

# 得到['ants', 'want']

低频词(Infrequent Words)

直觉上来看，如果一个词汇仅在语料库中出现一两次，那么它很有可能对于语义贡献较小，于是我们考虑移除这样的低频词。

1
2
3
4
5
vect = CountVectorizer(min_df=2)
vect.fit(malory)
print(vect.get_feature_names())

# ['ants', 'you']

N-grams模型

不难看出，上文提到的词袋法将词汇的顺序完全解体，这显然会产生一定的问题，因为很多时候词汇间存在关联，如”didn’t love” 和 “love” 之间的意义则完全不同。

考量到这种因素，我们采取N-grams模型，将原本的语料进行数目为N的配对，如N为2时，建立的Bigrams：

1
2
3
4
5
6
7
8
9
cv = CountVectorizer(ngram_range=(2, 2)).fit(malory)
print("Vocabulary size: {}".format(len(cv.vocabulary_)))
print("Vocabulary:\n{}".format(cv.get_feature_names()))


# 得到：
# Vocabulary size: 8
# Vocabulary:
# ['because that', 'do you', 'get ants', 'how you', 'that how', 'want ants', 'you get', 'you want']

N-gram有许多应用，我们最熟悉的应该就是搜索引擎的词汇联想：即当我们输入几个单词后，搜索引擎便会给出自动补全的问题猜测。当然，至于N-grams实现这一操作的数学原理，以及其深入的计算，本人就不研究了。

词频-逆文档频率(Term Frequency-Inverse Document Frecuency)

简称Tf-idf，这是一种评估一个词在整个模型中的重要程度的手段，基本思想是：

一个词在一句话中出现的次数越多，则越重要；同时如果其在整个语料库中出现的次数越多，则越不重要。

$TF-IDF(t,d) = TF(t,d) \cdot IDF(t)$

<br>

$IDF(t)=log\frac{1+n_{d}}{1+DF(d,t))}$

<br>

其中，

TF(Term Frequency, 词频)表示词条在一句话（文档）中出现的频率；

$n_{d}$为总文档数;

$DF(d,t)$ 为包含t词汇的文档数；

简而言之，Tf-idf倾向于过滤掉常见的词语，保留重要的词语。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.feature_extraction.text import TfidfVectorizer, TfidfTransformer

malory_tfidf = TfidfVectorizer().fit_transform(malory)
malory_tfidf.toarray()

# 得到：
# array([[ 0.41 , 0. , 0.576, 0. , 0. , 0. , 0.576, 0.41 ],
# 		 [ 0.318, 0.447, 0. , 0.447, 0.447, 0.447, 0. , 0.318]])

malory_tfidf = make_pipeline(CountVectorizer(),
							 TfidfTransformer()).fit_transform(malory)
malory_tfidf.toarray()

# 得到：
# array([[ 0.41 , 0. , 0.576, 0. , 0. , 0. , 0.576, 0.41 ],
#		 [ 0.318, 0.447, 0. , 0.447, 0.447, 0.447, 0. , 0.318]])

主题模型

前文所讲的词袋模型，存在一定的不足：

  1. 词语的句法特征无法捕捉

  2. 同义词无法捕捉

  3. 独热编码，因此特征数量很多

为了解决上述问题，便有了主题模型出现。

潜语义分析(Latent Semantic Analysis)

简称LSA，核心手法是运用截断奇异值分解(Truncated SVD)进行数据降维。

具体的数学原理本学渣搞不明白，也不想搞明白，就不深入研究了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.feature_extraction.text import CountVectorizer
vect = CountVectorizer(stop_words="english", min_df=4)
X_train = vect.fit_transform(text_train)
X_train.shape

# 得到原始的矢量化文本数据：
# (25000, 30462)

from sklearn.decomposition import TruncatedSVD
lsa = TruncatedSVD(n_components=100)
X_lsa = lsa.fit_transform(X_train)
lsa.components_.shape

# 得到100个话题的数据：
# (100, 30462)

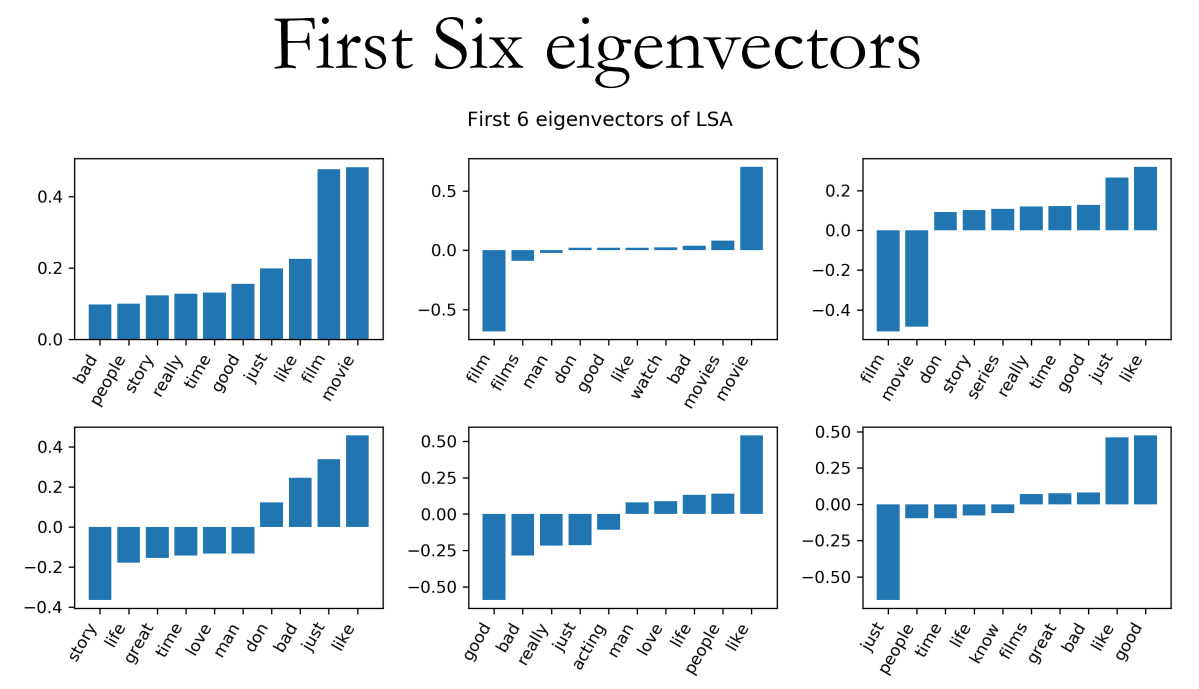
可以看出LSA易受非均衡数据的影响，因此有必要先进行放缩：

1
2
3
4
5
from sklearn.preprocessing import MaxAbsScaler
scaler = MaxAbsScaler()
X_scaled = scaler.fit_transform(X_train)
lsa_scaled = TruncatedSVD(n_components=100)
X_lsa_scaled = lsa_scaled.fit_transform(X_nscaled)

放缩后的特征重要性：

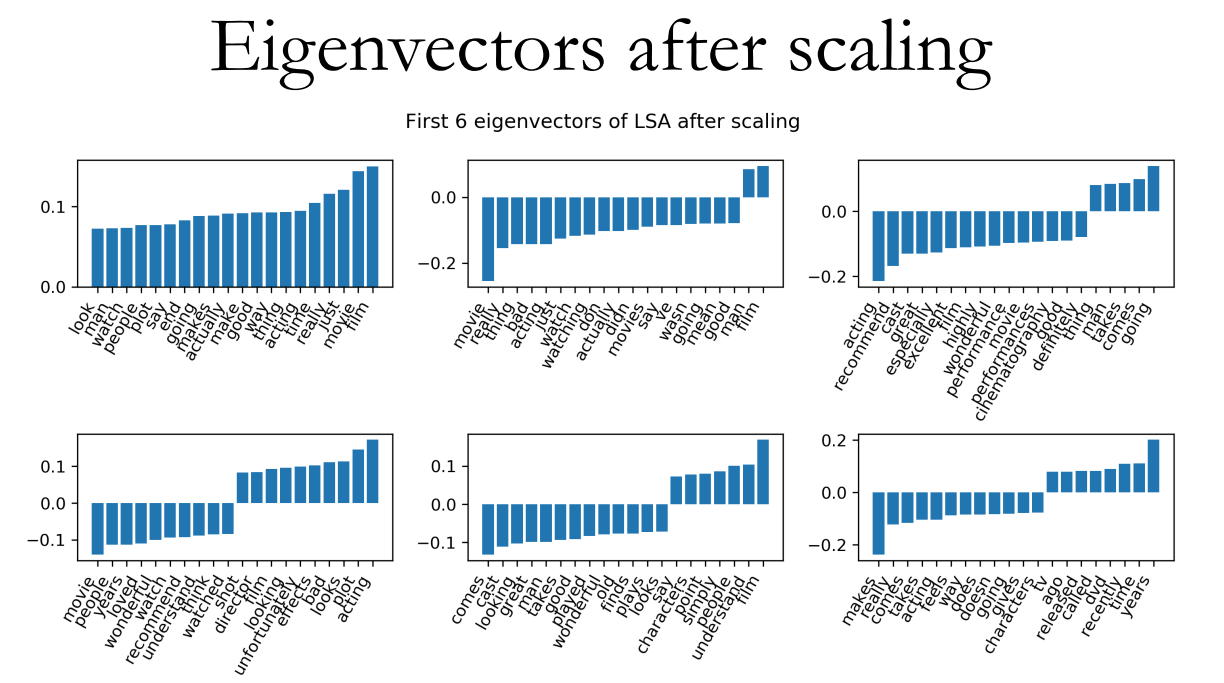
优点：
1）低维空间表示可以刻画同义词，同义词会对应着相同或相似的主题。
2）降维可去除部分噪声，使特征更优。
3）充分利用冗余数据。
4）无监督/完全自动化。
5）与语言无关。
缺点：
1）LSA可以处理向量空间模型无法解决的一义多词(synonymy)问题，但不能解决一词多义(polysemy)问题。因为LSA将每一个词映射为潜在语义空间中的一个点，也就是说一个词的多个意思在空间中对于的是同一个点，并没有被区分。
2）SVD的优化目标基于L-2 Norm 或者 Frobenius Norm 的，这相当于隐含了对数据的高斯分布假设。而 term 出现的次数是非负的，这明显不符合 Gaussian 假设，而更接近 Multi-nomial (多项)分布。
3）特征向量的方向没有对应的物理解释。
4）SVD的计算复杂度很高，而且当有新的文档来到时，若要更新模型需重新训练。
5）没有刻画term出现次数的概率模型。
6）对于count vectors 而言，欧式距离表达是不合适的（重建时会产生负数）。
7）维数的选择是ad-hoc的。
8）LSA具有词袋模型的缺点，即在一篇文章，或者一个句子中忽略词语的先后顺序。
9）LSA的概率模型假设文档和词的分布是服从联合正态分布的，但从观测数据来看是服从泊松分布的。因此LSA算法的一个改进PLSA使用了多项分布，其效果要好于LSA。

隐含狄利克雷分布(Latent Dirichlet Allocation)

简称LDA，这个模型涉及很多数学知识，本人不是专业研究这个领域的，就不搞什么知难而上了。总之就是基于一系列的运算，我们可以将语料库划分为预先设置好的话题数。这里仅记录下使用方法。

1
2
3
from sklearn.decomposition import LatentDirichletAllocation
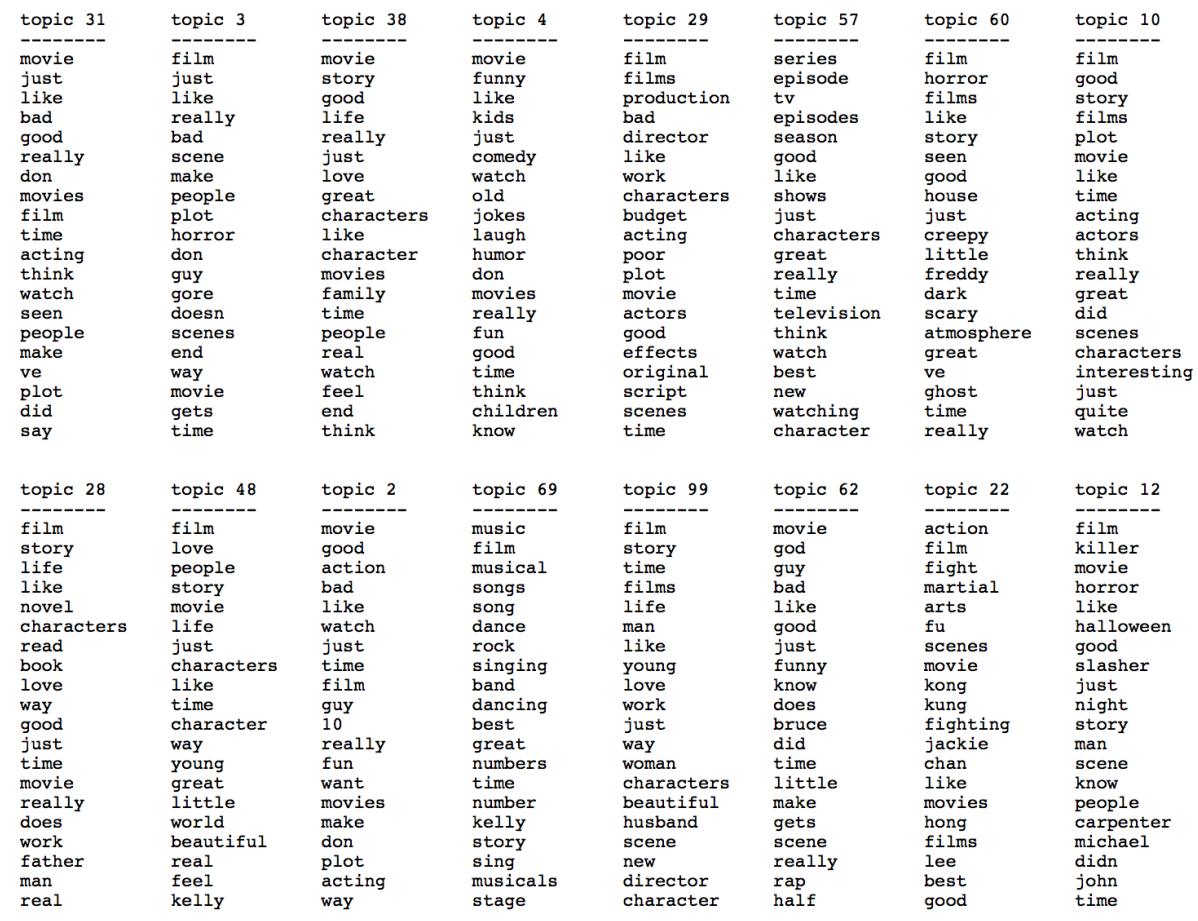
lda100 = LatentDirichletAllocation(n_components=100)
X_lda100 = lda100.fit_transform(X_train)

词嵌入(Word Embeddings)

似乎这一部分没有课时讲了，导致笔记没办法记录。那么自然语言处理部分就先到这了，算是小小地入了个门，等未来如果我有机会再学的话再补齐。

  • 连续词袋模型(Continuous Bag of Words)

    简称CBOW

    tbc……

  • 跳字模型(Skip-Gram)

    tbc……

  • Gensim

    tbc……

神经网络(Neural Networks)

神经网络，一个看起来很厉害的名字，就仿佛机器真的有了人脑的神经似的，单看这名字，还以为天网毁灭人类已经指日可待了，结果学了才知道，这名字原来只是个修辞层面的形容…

虽然各种百科上都自称神经网络算法受到了人脑神经元运转的启发，但依我说，这就是一群写百科的程序员胡扯出来的自我吹捧罢了，至少到目前为止，机器学习这领域本质上还是在做统计学的事情，机器也仍然一如既往地没有任何真正的智能存在，当然人工智能领域未来会怎么样我们不好说，但至少现今没必要觉得它有多神奇。

概述

从这一部分起，终于才算进到了较为前沿的算法领域。之前所记录的各种模型，说到底都是九十年代前就有了的，而时至今日，对于大体量的数据处理而言，神经网络的应用会更广泛些。

其实神经网络并不是一个与之前的模型完全不同的概念，比如说逻辑回归就可以看作一个单神经元的单层网络：

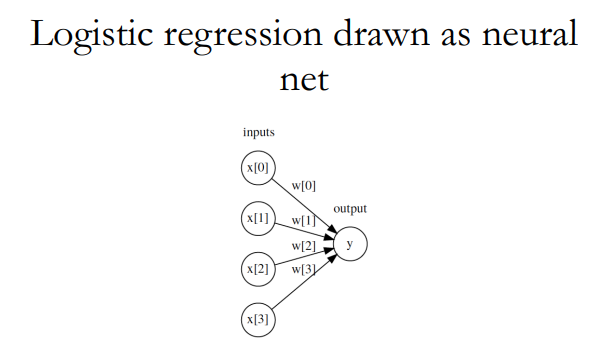
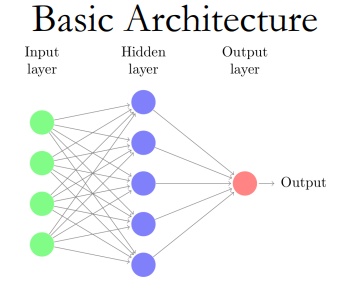
这样的结构被称为“感知机(Perceptron)”，其本身就已经是一个决策模型了，但是由于真实世界的复杂性，单一的模型无法胜任，我们便将多个感知机叠加多层，便成为了所谓的“神经网络”，这里其实就已经能看出来，这样的模型与人脑的神经结构差距大到完全没有可比性，本人更愿意用多层感知机(MLP)来称呼它，但谁让发明这个模型的人取了这么个名字呢，我们也就只能接受神经网络这一名词了。

激活函数(Activation Function)

激活函数是用来计算一个节点的输出的，如下图中的Activation所示：

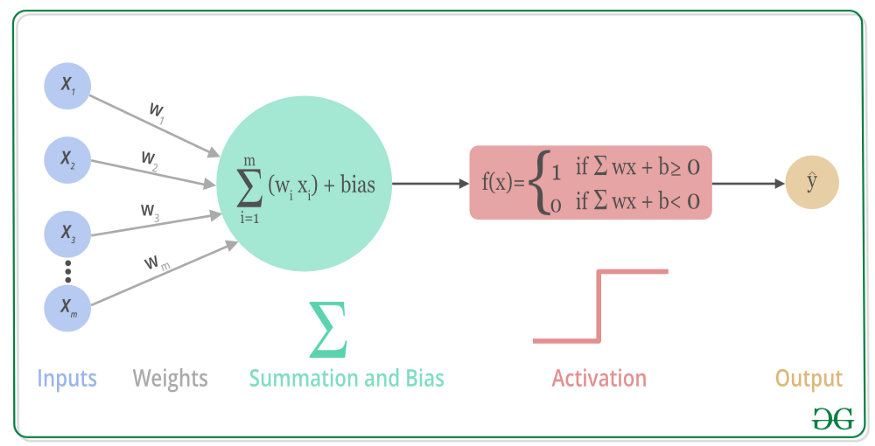
可以用作这一步的函数很多，既有线性也有非线性函数，如Sigmoid、Tanh、ReLU、Leaky ReLU、ELU、PReLU、Maxout、 Softplus，每一个都有其优劣，如Sigmond存在梯度消失的问题，且每个展开来都能写好几页，这里就不多深入了。

梯度下降算法(Gradient Descent)

梯度下降算法是神经网络模型训练中常用的优化算法，其目的是用来求目标函数的最小值。

根据计算目标函数采用数据量的不同，梯度下降算法又可以分为批量梯度下降算法（Batch Gradient Descent），随机梯度下降算法（Stochastic Gradient Descent）和小批量梯度下降算法（Mini-batch Gradient Descent）。

对于批量梯度下降算法，其是在整个训练集上计算的，如果数据集比较大，可能会面临内存不足问题，而且其收敛速度一般比较慢；对于随机梯度下降算法，又称为在线学习，收敛速度会快一些，但是有可能出现目标函数值震荡现象，因为高频率的参数更新导致了高方差；小批量梯度下降算法是折中方案，选取训练集中一个小批量样本计算，这样可以保证训练过程更稳定，而且采用批量训练方法也可以利用矩阵计算的优势。这是目前最常用的梯度下降算法。

那什么是梯度呢？简单来说，就是函数切线/切面/超平面切面上，指向函数极值方向的一个向量。数学上，就是函数的所有偏微分之和，具体的数学公式这里就不写了，对于入门理解有百害而无一利，这里放几张直观的图，可以帮助在宏观层面上理解即可，具体怎么算就交给热衷理论研究的大佬们搞了。

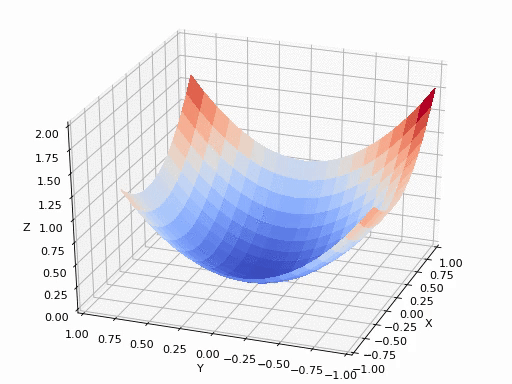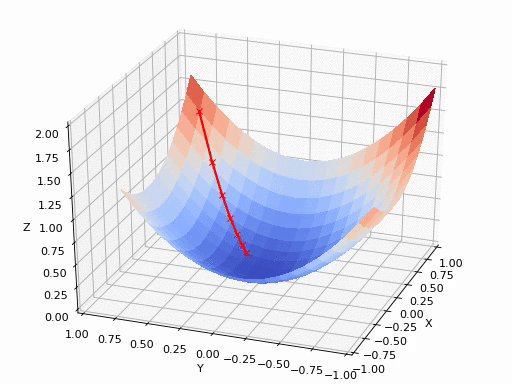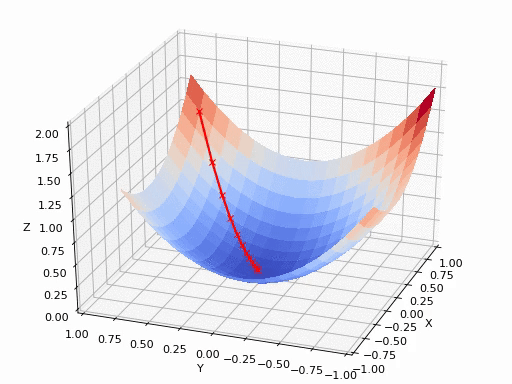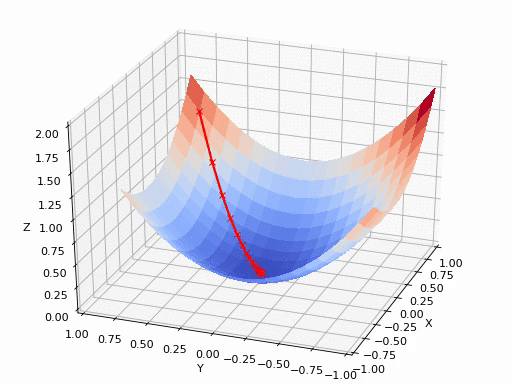
就很像在山顶放了一个球，一松手它就会顺着山坡最陡峭的地方滚落到谷底。

当然，梯度下降并非万能，像这样的有许多局部最优的函数，梯度下降就几乎无法找到全局最优点，这也很好理解：球滚到一个坑的底部时就不会再爬上去了，这就使其无法发现附近是否有更深的坑。

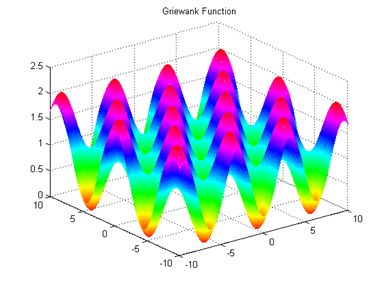
目前，梯度下降算法目前无法保证全局收敛也是一大问题，这里本学渣就不去管了，希望未来有理论大佬解决这一问题吧，

反向传播(Back Propagation)

反向传播，也叫BP算法，指的是在神经网络模型中，梯度下降算法的实现手段。

总在网上看到大佬说：

对于反向传播，简单的理解，它就是复合函数的链式法则

本人实在不才，不能理解这样的表述哪里简单，可能这就是专精数学的理科大佬的加密通话罢……

读了一些资料后，本人对于反向传播的理解大概如下：当我们给神经网络模型一组参数（也就是权重和偏误）后，这个模型便会得到一组预测数据，基于这组预测数据和实际数据，我们可以得到一个偏误值，接下来我们便希望降低偏误值，得到更优的模型。

而显然，影响偏误值、且我们能调整的，就是一开始给各个感知机的参数。由于每一层感知机的一部分参数是都由上一层的感知机传入，因此，为了调整某一层(n)的感知机，我们便需要先调整其上一层(n-1)的感知机，而为了调整上一层(n-1)的感知机，就需要调整更上一层(n-2)的感知机，这便出现了层层反推的效果，也就是所谓的“反向传播”。

在这样的思路下，我们首先将偏误值写为一个函数，然后对其求偏导，得到其梯度向量，然后通过设置学习率步长，使其逐步迭代至最优值。而在求偏导时，便会在反向传播的作用下，出现链式求导，最终作用到最外层参数。

这里的数学原理本人也不记录了，实在是十分十分的冗长，看多了脑袋疼。

TensorFlow

前面说了一堆理论的东西，对于本人来说其实没有什么用处，毕竟一方面本人的数学水平着实有限，看不太明白，另一方面本人没有搞理论研究的兴趣，看了对我也是浪费时间。这时候，其实我们需要的是一个能马上上手跑起来的东西，TensorFlow便是很好的选择。

TensorFlow是一个机器学习框架，简单的说，就是许多常用的底层算法，大佬们已经打包写好了，我们只需要调度就行，用搭房子比喻机器学习建模的话，TensorFlow就是提供了搭建房屋所用的木料，这样我们就不用从种树做起。

Keras

Keras是TensorFlow的官方高级API，对于初学者来说，Keras更简单易用。

实际使用时，像本人这种玩家级别的用户，使用Keras就足够了，没有必要过多深入TensorFlow本体。

使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from keras.models import Sequential
from keras.layers import Dense, Activation

model = Sequential([
 Dense(32, input_shape=(784,)),
 Activation('relu'),
 Dense(10),
 Activation('softmax')])
# or
model = Sequential()
model.add(Dense(32, input_dim=784))
model.add(Activation('relu'))
# or
model = Sequential([
 Dense(32, input_shape=(784,), activation='relu'),
 Dense(10, activation='softmax')])

卷积神经网络(Convolutional Neural Network)

简称CNN，当然不是那个整体搞意识形态输出新闻的CNN（不过话说回来，哪个媒体没有一定意识形态输出成分呢）。

当前的时代，卷积神经网络可以说是一个明星算法了，可能这个年代的人都对“卷”有着莫名的执着吧…

卷积神经网络最著名的是其在图象识别领域的应用。

卷积神经网络与一般的神经网络的区别在于：在将数据输入神经网络模型前，进行了“卷积”和“池化”的操作。

  • 卷积核(Convolution Kernel)

    “卷积”指的是基于一个“卷积核”矩阵进行的数据运算，具体的算法很简单，这里就不说了，而其背后的思想很复杂，这里也不多说了（说不明白），总而言之，一个图形经过卷积运算后，可以提取出一些特定的特征，有了这些特征，我们便可以将其交由神经网络模型来拟合。

    比如图片的“锐化”就是一个卷积运算的例子：

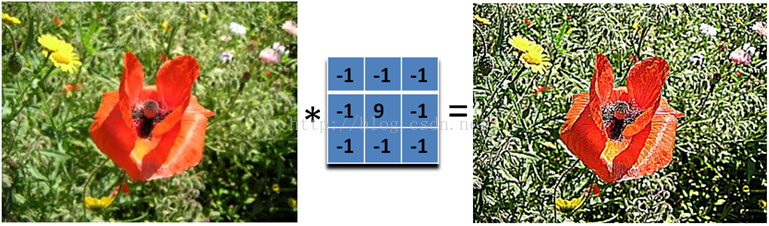
    或者这样的效果：

    不过具体为什么卷积核可以实现这样的效果，就会涉及到信号处理和一些微积分的知识，本人目前还没研究明白，这里先宏观层面记录下其效果。

    卷积核本质上是神经网络的参数，因此无需手动设定，神经网络会通过算法自动调整出最合适的卷积核。

  • 池化(Pooling)

    池化是进一步对卷积后的特征进行降维的操作，一般会用下述类型：平均池化(mean-pooling)，最大池化(max-pooling)、随机池化(Stochastic-pooling)和全局平均池化(global average pooling)，这一步可以节省显存的使用。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    from keras.models import Sequential
    from keras.layers import Conv2D, MaxPool2D
    from keras.layers import Dense, Flatten
    from keras.utils import to_categorical

    from keras.datasets import mnist
    (x_train, y_train), (x_test, y_test) = mnist.load_data()

    img_x, img_y = 28, 28
    x_train = x_train.reshape(x_train.shape[0], img_x, img_y, 1)
    x_test = x_test.reshape(x_test.shape[0], img_x, img_y, 1)

    x_train = x_train.astype('float32')
    x_test = x_test.astype('float32')
    x_train /= 255
    x_test /= 255

    y_train = to_categorical(y_train, 10)
    y_test = to_categorical(y_test, 10)

    model = Sequential()
    model.add(Conv2D(32, kernel_size=(5,5), activation='relu', input_shape=(img_x, img_y, 1)))
    model.add(MaxPool2D(pool_size=(2,2), strides=(2,2)))
    model.add(Conv2D(64, kernel_size=(5,5), activation='relu'))
    model.add(MaxPool2D(pool_size=(2,2), strides=(2,2)))
    model.add(Flatten())
    model.add(Dense(1000, activation='relu'))
    model.add(Dense(10, activation='softmax'))

    model.compile(optimizer='adam',
    			  loss='categorical_crossentropy',
    			  metrics=['accuracy'])

    model.fit(x_train, y_train, batch_size=128, epochs=10)

    score = model.evaluate(x_test, y_test)
    print('acc', score[1])

Drop Out

这一手段是为了解决神经网络容易出现的过拟合问题，简单来说就是删除某些感知机节点。

1
2
3
4
5
6
7
8
9
10
11
from keras.layers import Dropout
model_dropout = Sequential([
 Dense(1024, input_shape=(784,), activation='relu'),
 Dropout(.5),
 Dense(1024, activation='relu'),
 Dropout(.5),
 Dense(10, activation='softmax'),
])
model_dropout.compile("adam", "categorical_crossentropy", metrics=['accuracy'])
history_dropout = model_dropout.fit(X_train, y_train, batch_size=128,
 epochs=20, verbose=1, validation_split=.1)

递归神经网络(Recurrent Neural Network)

简称RNN，一般用于机器翻译。

1
2
3
4
5
6
7
8
9
10
11
12
model = keras.Sequential()
# Add an Embedding layer expecting input vocab of size 1000, and
# output embedding dimension of size 64.
model.add(layers.Embedding(input_dim=1000, output_dim=64))

# Add a LSTM layer with 128 internal units.
model.add(layers.LSTM(128))

# Add a Dense layer with 10 units.
model.add(layers.Dense(10))

model.summary()

时序预测(Time Series Forecast)

时序分析，算是个老朋友了，正巧本学期学了时间序列分析这门课，详见这几篇文章：[时序分析学习笔记（一）]、[时序分析学习笔记（二）]、[时间序列案例分析（一）——Lac Leman Festival De La Musique]

不过之前本人学习的时序知识都是基于R语言实现的，这里再记录下Python中的一些代码实现。

处理日期数据：

1
2
3
4
5
6
7
8
9
10
url = "ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_weekly_mlo.txt"
names = ["year", "month", "day", "year_decimal", "co2", "days", "1 yr ago", 
 "10 yr ago", "since 1800"]
maunaloa = pd.read_csv(url, skiprows=49, header=None, delim_whitespace=True,
 names=names, na_values=[-999.99])

# 或：
maunaloa = pd.read_csv(url, skiprows=49, header=None, delim_whitespace=True,
					   names=names, parse_dates=[[0, 1, 2]], na_values=[-999.99])

加索引：

1
2
3
maunaloa = pd.read_csv(url, skiprows=49, header=None, delim_whitespace=True,
 names=names, parse_dates=[[0, 1, 2]], na_values=[-999.99],
 index_col="year_month_day")

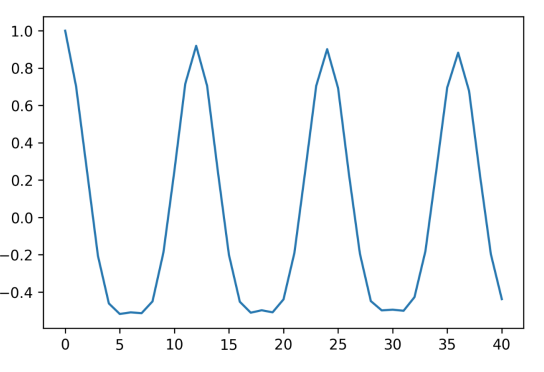
自相关：

1
ppm.autocorr()

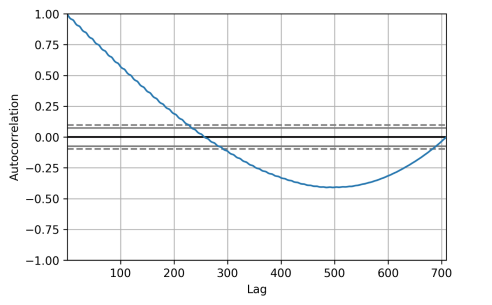
自相关函数：

1
2
3
from statsmodels.tsa.stattools import acf
autocorrelation = acf(ppm)
plt.plot(autocorrelation)
1
2
from pandas.tools.plotting import autocorrelation_plot
autocorrelation_plot(ppm)

差分序列自相关：

1
autocorrelation_plot(ppm.diff()[1:]) 
1
2
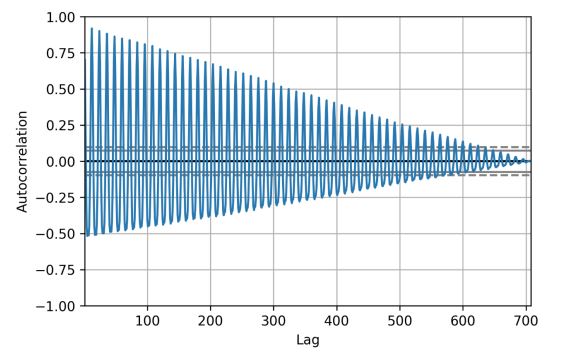
3
from statsmodels.tsa.stattools import acf
autocorrelation = acf(ppm.diff()[1:])
plt.plot(autocorrelation)

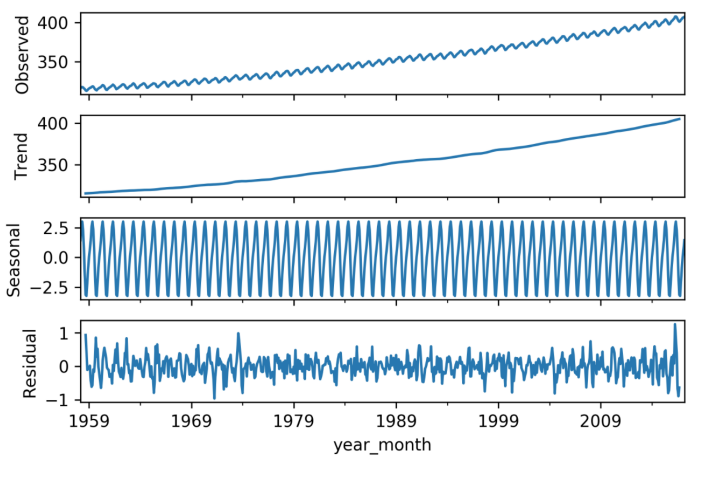
季节性数据拆分：

1
2
3
from statsmodels.tsa.seasonal import seasonal_decompose
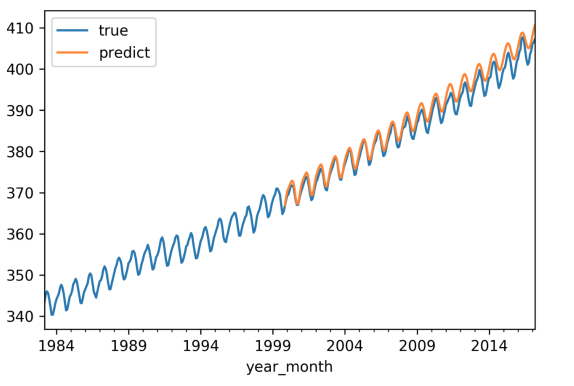
decomposition = seasonal_decompose(ppm, model='additive')
fig = decomposition.plot()

自回归模型(AR)：

1
2
3
4
5
6
7
from statsmodels.tsa import ar_model
ar = ar_model.AR(ppm[:500])
res = ar.fit(maxlag=12)

ppm[300:].plot(label="true")
res.predict(ppm.index[500], 
 ppm.index[-1]).plot(label="predict")

整合移动自回归模型(ARIMA)：

1
2
3
4
from statsmodels import tsa
arima_model = tsa.arima_model.ARIMA (ppm[:500], order=(12, 1, 0))
res = arima_model.fit()
arima_pred = res.predict(ppm.index[500], ppm.index[-1], typ="levels")

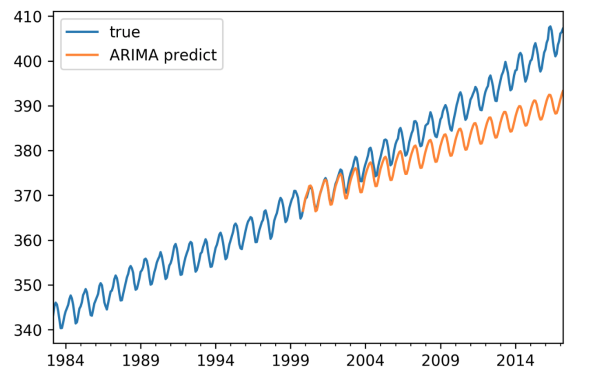
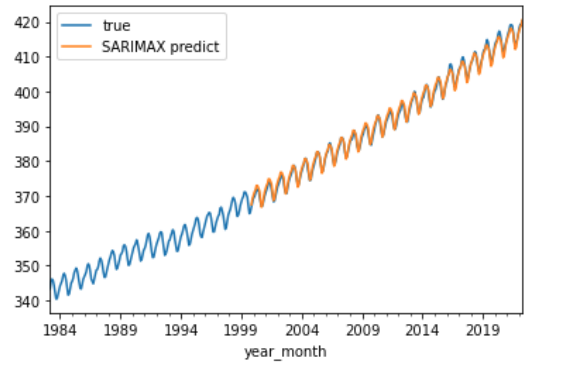
SARIMAX：

1
2
3
4
import statsmodels.api as sm
sar = sm.tsa.statespace.SARIMAX(ppm[:500], order=(0,0,0),
 seasonal_order=(0,1,0,12),trend='ct').fit()
fcst = sar.forecast(steps = len(ppm)-500)

Auto-ARIMA:

1
2
3
4
5
from pmdarima import auto_arima
model = pm.auto_arima(ppm[:500], max_p=7, max_d=2, max_q=7,
 max_P=4, max_D=2, max_Q=4, m=12, trace=True)
fcst, conf_int = model.predict(n_periods = len(ppm)-500, return_conf_int=True)
fcst = pd.Series(data=fcst, index=ppm.index[500:])

sklearn 预测

1
2
3
4
5
6
7
8
9
10
11
train = ppm[:500]
test = ppm[500:]
X = ppm.index.to_series().apply(lambda x: x.toordinal())
X = pd.DataFrame(X)
X_train, X_test = X.iloc[:500, :], X.iloc[500:, :]

from sklearn.linear_model import LinearRegression
lr = LinearRegression().fit(X_train, train)
lr_pred = lr.predict(X_test)
plt.plot(ppm.index, lr.predict(X))
ppm.plot()

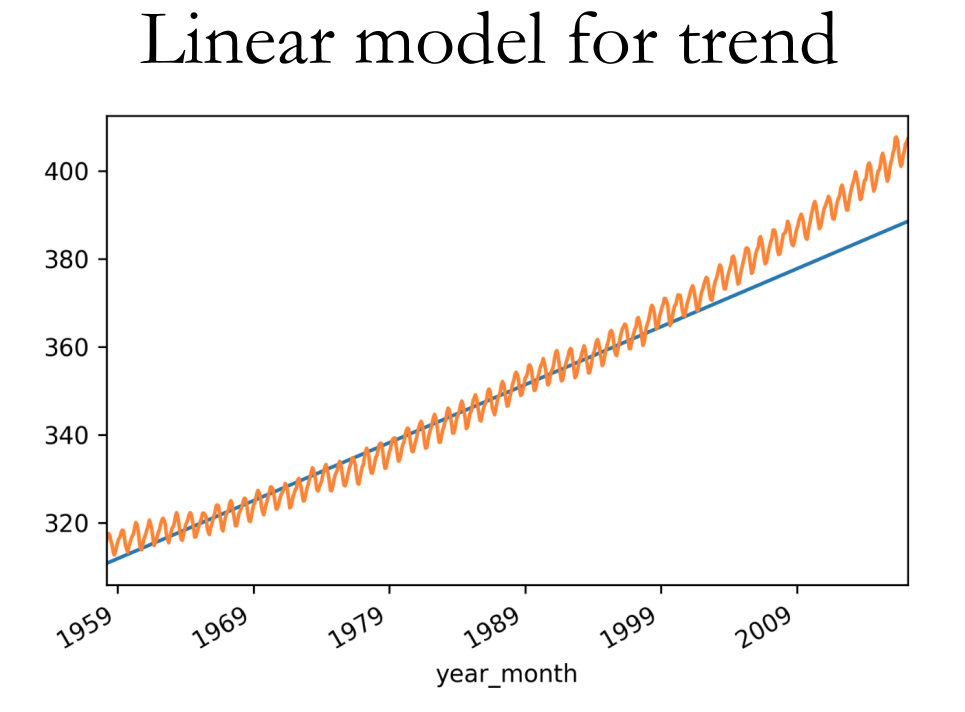
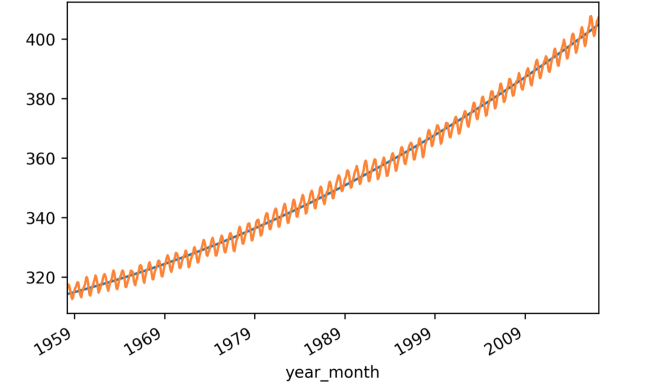
添加多项式特征：

1
2
3
4
5
6
from sklearn.preprocessing import PolynomialFeatures
lr_poly = make_pipeline(PolynomialFeatures(include_bias=False), 
 LinearRegression())
lr_poly.fit(X_train, train)
plt.plot(ppm.index, lr_poly.predict(X))
ppm.plot()

FBProphet

1
2
3
4
from fbprophet import Prophet
m = Prophet()
m.fit(fb_ppm[:500])
forecast = m.predict(fb_ppm)

未完待续…

后记

2022年11月28日更新：

在笔者写这篇后记时，这门课实际已经结课半年了。其实早在结课时，我就想把后记写了的，奈何怠惰缠身，一直就搁置着没做。而今天本人正好在为整个博客更新文章图片的引用格式，看到这里，想着索性就把后记顺手补全了。

学习机器学习这门课，于我来说是一门收获颇丰的记忆，当然，如果你看过我的笔记内容也不难发现，对于各种模型的许多底层数学知识，本学渣没有学的很透彻，所以坦白来讲，这门课并没有让我直接摇身一变，成为了可以通过相关知识来就业的人，恐怕对于许多人来说，这样的结果都会被归于“浪费时间”之列。然而对于我来说，在其中获得到的乐趣足以让我无悔于投入的时间。

当然，学完这门课，我对于机器行业的偏见仍然没什么变化，正如本人在前言中所说，机器学习中，尤其是如今流行的神经网络模型，对于我们来说，已经完全是黑盒了，模型的拟合性由于其内部成千上万的变量，对于人类来说，没有可读性，大家实际都不知道为什么一个模型有效，只是利用了“有效”这一结果，这样总让人联想到“炼丹”一类的玄学，如此的模式，我还是打心底难以认同，也对其未来的发展有些担忧。

但不管怎么说，倒腾数据、跑模型、调参数……这些都是很有趣的过程，虽说未来我大概很难有机会从事相关行业，具体的知识想必也会很快的被我遗忘，但是学习途中的所思所感，对我来说比记住某些数学公式更加珍贵。在这个时代，机器仿佛可以通过求数学最优解来学会很多东西：做数学题、下棋、识别图片，然而我想，有一件事情恐怕一时半会机器是无法学会的，那就是意识到：这个世界并非是一个必须追求最优的游戏，有时，以自己的方式来度过人生，要远比被强迫着追求“最优”的人生来的幸福的多。

以上是本人的一些意识流废话，如果你能看到这里，我要道一声谢谢，但我也要说，你可能是真的闲的没事干，建议你干点正事。Anyway，就让我们在别的什么地方再见吧。